zadání tutoriálu
Transkript
1
Numerické výpočty v jazyku Python
V minulém dı́le tutoriálu jsme se seznámili se základnı́mi pravidly syntaxe a programovanı́ v jazyce
Python. Popularita tohoto jazyka však nepramenı́ pouze z velmi pohodlné syntaxe, ale také z rozsáhlého
systému kvalitnı́ch knihoven – kolekcı́ užitečných algoritmů, funkcı́ a podprogramů či rozšı́řenı́. Cı́lem
tohoto tutoriálu bude naučit se použı́vat knihovny pro práci s numerickými daty. Stejně jako u minulého
dı́lu tutoriálu je tento dı́l dostupný ve formátu IPython Notebook (*.ipynb) na stránkách SVATu.
V tomto fotmátu si lze interaktivně vyzkoušet přı́kazy i následně vypracovat úlohy.
V tomto dı́le tutoriálu se podrobněji seznámı́me s jednou z nejdůležitějšı́ch vědeckých knihoven,
NumPy (Numerical Python). Tato knihovna poskytuje algoritmy a datové typy (třı́dy) určené pro práci
s vektory, maticemi a jinými matematickými konstrukty. Na knihovně NumPy jsou založeny dalšı́ populárnı́
vědecké knihovny jako SciPy (pokročilé vědecké a výpočetnı́ algoritmy) a Matplotlib (vytvářenı́ grafů),
se kterými se seznámı́me v dalšı́ch dı́lech tutoriálu.
Knihovna NumPy dnes tvořı́ základ většiny vědeckých i jiných programů psaných v jazyce Python, proto většinou nenı́ problém ji nainstalovat. Pokud jste Python instalovali pomocı́ distribuce Anaconda, je knihovna NumPy již nainstalovaná. Většina distribucı́ jazyka Python (včetně
balı́čkovacı́ch systémů GNU/Linux distribucı́) tuto knihovnu umožňuje doinstalovat. Obvykle má jméno
podobné python-numpy. Přehledná dokumentace knihovny je na http://docs.scipy.org/doc/numpy/
reference/, kde za zmı́nku stojı́ sekce Routines, která dokumentuje různé užitečné funkce.
2
Moduly
Vysvětleme si, co je to v Pythonu modul (knihovna). Při programátorské práci se často hodı́ uložit si
kód definujı́cı́ funkce nebo data do samostatných souborů. Z těch pak lze tento kód importovat (nahrát)
např. do IPython notebooku a nenı́ nutné jej pokaždé znova ručně zadávat. V jazyce Python se takové
soubory s hotovým kódem nazývajı́ moduly (knihovny) a obvykle majı́ koncovkou *.py.
Data a funkce lze ze souboru muj modul.py importovat přı́kazem import muj modul. (Soubor
muj modul.py se přitom musı́ nacházet v jedné ze složek, kde Python hledá moduly.) Po importovánı́ budou funkce a data definovaná v tomto modulu přı́stupná jako atributy objektu muj modul,
jenž tento modul reprezentuje. Např. funkci moje funkce z modulu muj modul lze zavolat jako
muj modul.moje funkce(). (Navzdory podobné syntaxi se nejedná o metodu objektu muj modul).
V následujı́cı́m přı́kladě importujeme modul sys, který obsahuje data, nastavenı́ a jiné funkce interpreteru jazyka Python. Např. sys.path je seznam složek, ve kterých bude interpreter hledat moduly (ty
se na různých počı́tačı́ch mohou velmi lišit).
In [1]: import sys
sys.path.insert(0, ’.’)
sys.path
# pridame aktualni slozku na zacatek seznamu
Out[1]: [’.’,
’’,
’/home/ondrej/compass/sw projects/CDB-hg/src’,
’/home/ondrej/compass/sw projects/python-lib’,
’/home/ondrej/school/SVAT/python tutorial/numpy’,
’/home/ondrej/anaconda/envs/py3k/lib/python33.zip’,
’/home/ondrej/anaconda/envs/py3k/lib/python3.3’,
’/home/ondrej/anaconda/envs/py3k/lib/python3.3/plat-linux’,
’/home/ondrej/anaconda/envs/py3k/lib/python3.3/lib-dynload’,
’/home/ondrej/anaconda/envs/py3k/lib/python3.3/site-packages’,
’/home/ondrej/anaconda/envs/py3k/lib/python3.3/site-packages/Sphinx-1.3.1-py3.3.egg’,
’/home/ondrej/anaconda/envs/py3k/lib/python3.3/site-packages/cryptography-0.9.1-py3.3-linux’/home/ondrej/anaconda/envs/py3k/lib/python3.3/site-packages/setuptools-17.1.1-py3.3.egg’,
’/home/ondrej/anaconda/envs/py3k/lib/python3.3/site-packages/IPython/extensions’,
’/home/ondrej/.ipython’]
Moduly mohou být zařazeny do hierarchické struktury tzv. balı́čků. Obvykle se jedná o hierarchii
složek a podsložek. Např. modul request z balı́ku urllib lze nahrát přı́kazem import urllib.request
1
Standardnı́ knihovna balı́čků a modulů (obvykle) distribuovaná společně s interpretem obsahuje
mnoho užitečných funkcı́ a běžné použı́vaných algoritmů. Přehled a dokumentace je na https://docs.
python.org/3/library/. Dodatečné balı́čky lze většinou najı́t a zı́skat na https://pypi.python.org/.
3
Typ ndarray z knihovny NumPy
Většina numerických výpočtů ve vědě spočı́vá v opakovanı́ nějakých operacı́ s čı́sly, např. výpočet aritmetického průměru nebo operace s vektory a maticemi. Toto opakovánı́ se obvykle provádı́ tak, že dané
operace jsou vykonávány po řadě pro všechny prvky nějakého pole čı́sel. Nabı́zelo by se použı́t datový
typ list (seznam) pro reprezentaci seznamu čı́sel a operace provádět opakovaně ve for cyklu.
Tento přı́stup však vyžaduje, aby každé opakovánı́ bylo interpretováno zvlášt’ a to může být pro velké
seznamy pomalé. Proto je výhodné použı́t jiný datový typ, který umožňuje opakované operace delegovat
na funkce kompilovaných knihoven, které jsou mnohem rychlejšı́. K tomu sloužı́ právě základnı́ datový
typ ndarray (pole) z modulu NumPy, který je určen k reprezentaci polı́ čı́sel.
V následujı́cı́m přı́kladu importujeme knihovnu NumPy. Použı́vı́me přitom formu import numpy as
np, která pomocı́ klı́čového slova as umožňuje rovnou specifikovat jméno objektu reprezentujı́cı́ho modul.
To se hodı́, pokud často použı́váme modul s delšı́m jménem.
In [2]: import numpy as np
3.1
Vytvářenı́ polı́ čı́sel
Objekt typu (třı́dy) ndarray lze z existujı́cı́ch dat vytvořit pomocı́ funkce np.array, která převede
argument reprezentujı́cı́ seznam čı́sel na typ pole. Takto lze např. vytvořit 1D pole (řádkový vektor) ze
seznamu čı́sel.
In [3]: cisla = [1, 2, 5, 9, 9, 8, 7]
radkovy_vektor = np.array(cisla)
radkovy_vektor
Out[3]: array([1, 2, 5, 9, 9, 8, 7])
Interpreter dle obvyklé konvence reprezentuje objekty typu ndarray pomocı́ kódu, který lze použı́t
k jejich vytvořenı́. Ačkoliv tedy vypisuje array(...), jedná se skutečně o objekt typu ndarray. Zkontrolujme to pomocı́ funkce type:
In [4]: type(radkovy_vektor)
Out[4]: numpy.ndarray
3.1.1
Parametrizované vytvářenı́ polı́ čı́sel
Knihovna NumPy poskytuje užitečné funkce pro vytvářenı́ posloupnosti čı́sel nebo intervalu podle zadaných parametrů. Běžně je např. potřeba vytvořit pole obsahujı́cı́ čı́sla od i až po n. K tomu sloužı́
funkce np.arange, která je analogiı́ funkce range, pouze vracı́ objekt typu ndarray.
In [5]: np.arange(2, 16, 2)
Out[5]: array([ 2,
4,
6,
# pole cisel od 2 do 16 (prvni vcetne, druhe ne vcetně) s krokem 2
8, 10, 12, 14])
Pole lze také vytvořit výběrem n stejně vzdálených čı́sel z intervalu ha, bi (ve výchozı́m nastavenı́
funkce včetně koncových bodů). K tomu sloužı́ funkce np.linspace:
In [6]: np.linspace(3.5, 4, 5)
# 5 stejne vzdalenych cisel z intervalu <3.5, 4>
Out[6]: array([ 3.5
3.75 ,
,
3.625,
3.875,
4.
])
Pole obsahujı́cı́ n čı́sel rovných 0 lze vytvořit pomocı́ funkce np.zeros:
In [7]: np.zeros(10)
Out[7]: array([ 0.,
# pole obsahujici 10 cisel 0
0.,
0.,
0.,
0.,
0.,
2
0.,
0.,
0.,
0.])
3.2
Vı́cerozměrná pole a dimenze
Při numerických výpočtech je často vhodné použı́t 2D pole čı́sel neboli matice. Matici lze vytvořit pomocı́
funkce np.array tı́m, že jako argument dáme seznam (nebo n-tici – tuple –, hlavně to musı́ být sekvence)
seznamů (n-tic) s čı́sly. Tato struktura představuje matici po řádcı́ch.
In [8]: matice = np.array([
[1, 2, 3],
[4, 9, 7],
[15, 16, 8]
])
matice
Out[8]: array([[ 1, 2,
[ 4, 9,
[15, 16,
3],
7],
8]])
Každý objekt typu ndarray má atribut shape. Jedná se o n-tici čı́sel určujı́cı́ počet prvků v každé
z n dimenzı́ (rozměrů) pole:
In [9]: matice.shape
Out[9]: (3, 3)
Dimenzı́ (rozměrem) se zde myslı́ každý nezávislý indexovacı́ směr v poli čı́sel. Počet dimenzı́ je
dostupný v atributu ndim a, jak by se dalo čekat, je roven délce n-tice v atributu shape:
In [10]: matice.ndim == len(matice.shape)
Out[10]: True
Dimenzi a rozměry pole lze měnit pomocı́ metody reshape, již majı́ všechny objekty typu ndarray.
Jejı́ argument je n-tice odpovı́dajı́cı́ požadovanému atributu shape.
In [11]: matice.reshape((9,))
Out[11]: array([ 1,
2,
3,
4,
9,
7, 15, 16,
8])
Ačkoliv tato metoda vrátı́ nový objekt, tento objekt se stále odkazuje na data původnı́ho objektu a
pouze použı́vá jiné indexovánı́ (“pohled” na objekt). Nové a původnı́ rozměry musı́ být kompatibilnı́,
tedy součin prvků obou n-tic musı́ být stejný. Pro vytvořenı́ nového pole je potřeba explicitně zavolat
metodu ndarray.copy.
3.3
Vektorizované operace
Jak už bylo řečeno v úvodu, pole čı́sel sloužı́ předevšı́m k rychlému opakovánı́ operacı́ na jeho prvcı́ch.
Oproti klasickému seznamu čı́sel lze např. mnohem jednodušeji vyjádřit “vynásob každý prvek dvěma”
a výpočet je také mnohem rychlejšı́.
In [12]: radkovy_vektor * 2
Out[12]: array([ 2,
4, 10, 18, 18, 16, 14])
Obdobně lze vyjádřit (∀i ∈ {1, . . . , n})(yi = xi + xi · 2):
In [13]: y = radkovy_vektor + radkovy_vektor * 2
y
Out[13]: array([ 3,
6, 15, 27, 27, 24, 21])
3
Protože tyto operace připomı́najı́ operace s vektory (vektory a matice si můžete zopakovat na úloze
3.4 v 3. sérii SVAT ročnı́ku 2014), nazývá se toto skrytı́ explicitnı́ho for cyklu “vektorizace operace”.
Vektorizace zafunguje na většinu operátorů pro práci s čı́sly. Výsledkem je vektor stejné délky jako
argument s prvky odpovı́dajı́cı́ výsledkům operacı́.
Vektorizovat lze i běžné matematické funkce s pomocı́ speciálnı́ch funkcı́ (objekty typu ufunc) z modulu NumPy.
In [14]: np.sin(radkovy_vektor)
Out[14]: array([ 0.84147098,
0.98935825,
# sin() všech prvků pole
0.90929743, -0.95892427,
0.6569866 ])
0.41211849,
0.41211849,
Použitı́m vektorizovaných operacı́ nebo funkcı́ v definici funkce automaticky dostáváme vektorizovanou funkci, např. při zadefinovánı́ funkce f (x) = sin(x2 ) · exp(−x):
In [15]: def f(x):
return np.sin(x**2) * np.exp(-x)
f(radkovy_vektor)
Out[15]: array([
3.09559876e-01, -1.02422080e-01,
-7.77343540e-05, -7.77343540e-05,
-8.69709844e-04])
-8.91779077e-04,
3.08634353e-04,
Pokud funkci f dáme jako argument pouze jedno čı́slo, výpočet také proběhne v pořádku, protože
čı́slo samotné (skalár) je bráno jako pole o dimenzi 0.
In [16]: f(62)
Out[16]: -1.1448107391570701e-27
Argumenty, které chceme interpretovat jako pole čı́sel, lze ve funkci konvertovat na pole pomocı́
funkce np.asarray, která funguje podobně jako np.array, ale snažı́ se co nejméně kopı́rovat data. Po
této úpravě bude funkce f schopná vzı́t jako argument i seznam (list) či n-tici (tuple).
In [17]: def f(x):
x = np.asarray(x)
return np.sin(x**2) * np.exp(-x)
f([7, 2, 4])
Out[17]: array([-0.00086971, -0.10242208, -0.00527313])
3.3.1
Rozšı́řenı́ dimenze při vektorizovaných operacı́ch
Pokud se provádı́ vektorizovaná operace mezi poli nestejné dimenze, ale sdı́lejı́cı́mi některé rozměry, jsou
pole s chybějı́cı́mi rozměry v těchto rozměrech “virtuálně nakopı́rována”, jak je vidět na přı́kladě:
In [18]: vektor_3 = np.arange(3) # řádkový vektor [0, 1, 2]
matice * vektor_3 # pro každý řádek matice je "nakopı́rován" vektor_3
Out[18]: array([[ 0, 2, 6],
[ 0, 9, 14],
[ 0, 16, 16]])
Pokud bychom chtěli “kopı́rovat” po sloupcı́ch, musı́me použı́t sloupcový vektor
In [19]: vektor_3_sloupec = vektor_3.reshape((3, 1))
vektor_3_sloupec
Out[19]: array([[0],
[1],
[2]])
In [20]: matice * vektor_3_sloupec
Out[20]: array([[ 0, 0, 0],
[ 4, 9, 7],
[30, 32, 16]])
4
# pole o 3 radcich a 1 sloupci
3.4
Indexovánı́ polı́
Objekty typu ndarray lze indexovat podobně jako objekty typu list (seznam) nebo str (řetězec znaků)
pomocı́ indexovacı́ho operátoru []. Stále platı́, že prvnı́ prvek pole má index 0.
In [21]: radkovy_vektor[5]
# paty prvek v poli pocitany podle konvence "nulty, prvni, druhy..."
Out[21]: 8
Narozdı́l od běžných datových typů (list, str) však vybránı́ podmnožiny pomocı́ operátoru []
nevrátı́ objekt s kopiı́ původnı́ch dat, ale pouze “pohled” na podmnožinu původnı́ch dat (podobně jako u
reshape). Podmnožinu lze vybrat podobně jako u objektů typu list zápisem pole[start:stop:step].
In [22]: radkovy_vektor[2:6:2]
# od 2. prvku do 6. (ne vcetne) s krokem 2
Out[22]: array([5, 9])
Podmnožinu lze vybrat také tı́m, že operátoru [] předáme seznam nebo pole indexů.
In [23]: zajimave_indexy = [1, 4, 6] # zajimaji nas tyto pozice v poli
radkovy_vektor[zajimave_indexy]
Out[23]: array([2, 9, 7])
Alternativně lze podmnožinu vybrat tak, že operátoru [] předáme pole o stejné délce jako indexované
pole, které obsahuje pouze hodnoty True a False. Ty určujı́, zda daný prvek má být vybrán či ne.
Takováto pole podobná maskám se dajı́ jednoduše vyrobit pomocı́ porovnávacı́ch operátorů.
In [24]: je_sude_maska = (radkovy_vektor % 2) == 0
je_sude_maska
# zbytek po deleni 2 je 0
Out[24]: array([False,
True, False], dtype=bool)
True, False, False, False,
In [25]: radkovy_vektor[je_sude_maska]
Out[25]: array([2, 8])
Pro 2D pole (přı́padně vı́cerozměrná pole) fungujı́ stejná indexovacı́ pravidla jako u řádkových vektorů, avšak jednotlivé indexovacı́ úkony jsou v operátoru [] pro každou dimenzi odděleny čárkou. Takto
lze např. vybrat podmnožinu matice od 2. řádku dál a pouze 1. a 3. sloupec:
In [26]: zajimave_sloupce = [0, 2]
matice[1:,zajimave_sloupce]
Out[26]: array([[ 4,
[15,
3.5
7],
8]])
Kumulativnı́ funkce
Často se hodı́ redukovat vektor na jedno čı́slo, např. najı́t jeho maximum, minimum nebo průměr. K tomu
sloužı́ tzv. kumulativnı́ metody, které všechna čı́sla vektoru dle nějakého algoritmu akumulujı́ do jednoho
čı́sla. Objekty typu ndarray majı́ takových metod několik, např. mean pro aritmetický průměr.
In [27]: radkovy_vektor.mean()
Out[27]: 5.8571428571428568
Mezi dalšı́ kumulativnı́ metody objektu ndarray patřı́:
metoda
význam
min
minimum
max
maximum
5
metoda
význam
argmin
index minima
argmax
index maxima
std
směrodatná odchylka
sum
součet prvků
prod
součin prvků
all
všechny prvky jsou rovny True
any
alespoň jeden prvek je roven True
Tyto kumulativnı́ metody obvykle akumulujı́ všechny prvky pole nezávisle na dimenzi, ale pokud
dostanou nepovinný argument axis označujı́cı́ index dimenze (indexováno od 0 v souladu s atributem
shape), akumulujı́ pouze přes tuto dimenzi, čı́mž tuto dimenzi efektivně odstranı́. Takto lze spočı́tat např.
průměr každého ze sloupců matice – jednotlivé řádky (prvnı́ dimenze – index 0) jsou tak redukovány na
jednu hodnotu.
In [28]: matice.mean(axis=0)
Out[28]: array([ 6.66666667,
9.
,
6.
])
V modulu NumPy se nacházejı́ i dalšı́, podobné funkce, které však nemajı́ svůj protějšek jako metoda
třı́dy ndarray. Medián pole tak např. spočteme funkcı́ np.median(pole), ale nikoli jako pole.median().
4
Reálné aplikace knihovny NumPy
V této kapitole si ukážeme některé jednoduché aplikace třı́dy ndarray a dalšı́ch užitečných funkcı́
z knihovny NumPy.
4.1
Řešenı́ soustavy rovnic pomocı́ matic a vektorů
Lineárnı́ soustavy rovnic typu
3x + 2y − z =
1
(1)
2x − 2y + 4z = −2
(2)
−x +
1
2y
− z=
0
(3)
lze vyjádřit pomocı́ matic a vektorů jako rovnici
A~x = ~b,
kde
3
A= 2
−1
2 −1
x
1
−2 4 , ~x = y , ~b = −2 .
0.5 −1
z
0
A~x zde značı́ maticové násobenı́, pro zopakovánı́ znovu doporučujeme úlohu 3.4 z ročnku 2014 SVAT
(viz výše).
Zadefinujme si objekty se zadanými čı́sly pomocı́ objektů typu ndarray.
In [29]: A = np.array([
[3, 2, -1],
[2, -2, 4],
[-1, 0.5, -1]
])
b = np.array([-1 ,-2, 0])
6
Řešenı́ (za předpokladu, že existuje) najdeme pomocı́ funkce np.linalg.solve (podbalı́ček
numpy.linalg obsahuje funkce pro lineárnı́ algebru).
In [30]: x = np.linalg.solve(A, b)
x
Out[30]: array([ 1.
, -3.33333333, -2.66666667])
Pokud by řešenı́ neexistovalo, vyhodı́ tato funkce chybu (výjimku). Pak by šlo zı́skat alespoň přibližnou
aproximaci řešenı́ pomocı́ funkce np.linalg.pinv, která vypočı́tá aproximaci inverznı́ matice Ã−1 a
řešenı́ pak aproximuje jako ~x̃ = Ã−1~b (vlnka nad A značı́ aproximaci).
Výsledek můžeme otestovat pomocı́ maticového součinu A~x. Výraz A * x by však pouze vypočı́tal
násobenı́ po prvcı́ch. Pro maticový součin je potřeba použı́t metodu dot (“tečka” - součin) objektu typu
ndarray:
In [31]: A.dot(x)
# maticovy soucin Ax
Out[31]: array([ -1.00000000e+00,
-2.00000000e+00,
4.44089210e-16])
Poslednı́ prvek výsledku neodpovı́dá přı́mo nule, protože při numerických operacı́ch na čı́slech s omezenou přesnostı́ docházı́ k částečnému zaokrouhlovánı́. V tomto přı́padě bylo čı́slo 2.6 s periodickým desetinným rozvojem někde zaokrouhleno na 2.6666 . . . 667 a tato nepřesnost se pak promı́tla do výsledku.
Nicméně pro běžné výpočty je čı́slo řádu 10−16 zaměnitelné s nulou a v tomto přı́padě tato nepřesnost
nenı́ kritická. V důležitých výpočtech s mnoha mezivýsledky se však na toto riziko nesmı́ zapomı́nat.
4.2
Načı́tánı́ a zápis matic z/do souboru
Knihovna NumPy poskytuje užitečné funkce np.loadtxt, resp. np.savetxt pro načı́tánı́, resp. zápis matic
z/do textových souborů. Matici A lze do souboru matice A.txt uložit takto:
In [32]: jmeno_souboru = ’matice_A.txt’
np.savetxt(jmeno_souboru, A)
Můžeme se přesvědčit, že tento soubor skutečně obsahuje matici. Protože byly funkci np.savetxt
ponechány výchozı́ parametry, jsou čı́sla v textovém souboru oddělena mezerou.
In [33]: soubor = open(jmeno_souboru, ’r’)
for radek in soubor:
print(radek, end=’’) # radky uz obsahuji ukoncovaci znak
soubor.close()
3.000000000000000000e+00 2.000000000000000000e+00 -1.000000000000000000e+00
2.000000000000000000e+00 -2.000000000000000000e+00 4.000000000000000000e+00
-1.000000000000000000e+00 5.000000000000000000e-01 -1.000000000000000000e+00
Čı́sla jsou uložena s explicitnı́m desetinným rozvojem, ale pro načı́tánı́ nenı́ toto nutné. Nynı́ můžeme
využı́t funkci np.loadtxt pro nahránı́ těchto maticových/tabulkových dat z textového souboru:
In [34]: A_2 = np.loadtxt(jmeno_souboru)
np.allclose(A, A_2)
Out[34]: True
V poslednı́m řádku jsme použili funkci np.allclose, která porovnává rovnost dvou polı́ prvek po
prvku v rámci numerické přesnosti.
Existujı́ také funkce np.load a np.save, které se volajı́ podobně, ale ukládajı́ do binárnı́ch souborů
s koncovkou *.npy. Zápis a načı́tánı́ je s tı́mto formátem rychlejšı́, avšak jiné programy ho nemusejı́ umět
přečı́st, zatı́mco textový soubor s největšı́ pravděpodobnostı́ přečtou všechny.
7
4.3
Převod mezi čı́selnými soustavami
Přirozená čı́sla lze obecně zapisovat v různých čı́selných soustavách s různými bázemi b ∈ N. Obecně pak
můžeme vyjádřit čı́slo x jako
x = an bn + · · · + a2 b2 + a1 b1 + a0 b0 =
n
X
a i bi ,
i=0
kde ai je koeficient před i-tou mocninou báze b, ai ∈ {0, 1, . . . , b − 1}. Pokud b = 10, jedná se o běžně
použı́vanou desı́tkovou soustavu, např. 152 = 100 + 50 + 2 = 1 · 102 + 5 · 101 + 2 · 100 . Pokud b > 10,
obvykle se k čı́slicı́m přidávajı́ ještě pı́smena abecedy. Např. při práci s pamětı́ počı́tače se často použı́vá
šestnáctková soustava s b = 16 a čı́slicemi ai ∈ {0, 1, . . . , 9, A, B, C, D, E, F } (obvykle se nerozlišujı́ velká
a malá pı́smena). Jak už vı́me, v jazyku Python lze pomocı́ funkce int převést řetězec představujı́cı́
přirozené čı́slo na přirozené čı́slo:
In [35]: int(’15454’)
Out[35]: 15454
Této funkci lze ale dát i druhý (nepovinný) argument představujı́cı́ bázi b:
In [36]: int(’15af’, 16)
Out[36]: 5551
Můžeme se přesvědčit, že to je skutečně správný výsledek.
In [37]: b = 16
1 * b**3 + 5 * b**2 + 10 * b**1 + 15 * b**0
Out[37]: 5551
Převod přirozeného čı́sla z desı́tkové soustavy na řetězec reprezentujı́cı́ čı́slo v libovolné soustavě
umožňuje funkce np.base repr.
In [38]: np.base_repr(5551, 16)
Out[38]: ’15AF’
5
5.1
Úlohy
1. úloha (1b): Rotace vektoru kolem 3. osy
Definujte funkci, která jako prvnı́ argument vezme úhel ve stupnı́ch a jako druhý argument vektor
v trojrozměrném prostoru (tedy 1D pole o 3 prvcı́ch). Tato funkce pak vytvořı́ matici Rz rotace kolem
osy z zadefinované v úloze 3.4 z ročnı́ku 2014 SVAT (viz výše) a pomocı́ nı́ vypočı́tá a vrátı́ vektor
zrotovaný o požadovaný úhel. Může se hodit funkce np.deg2rad pro převod stupňů na radiány.
5.2
2. úloha (1b): Řešitel soustavy lineárnı́ch rovnic
Definujte funkci, která jako argument vezme jméno textového souboru, ze kterého načte matici. Poslednı́
sloupec matice bude odpovı́dat vektoru ~b a zbytek matice před tı́mto sloupcem bude odpovı́dat matici
A. Funkce vrátı́ vektor ~x, který je řešenı́m rovnice
A~x = ~b
za předpokladu, že existuje řešenı́ (jinak může vyhodit chybu).
8
5.3
3. úloha (1b): Binárnı́ operace na čı́slech v obecných soustavách
Definujte funkci, která jako argumenty po řadě vezme:
1.
2.
3.
4.
funkci z modulu operator reprezentujı́cı́ binárnı́ operaci, např. operator.add(1, 2) == (1 + 2)
řetězec znaků reprezentujı́cı́ čı́slo v dané soustavě pro levou stranu operace
řetězec znaků reprezentujı́cı́ čı́slo v dané soustavě pro pravou stranu operace
přirozené čı́slo reprezentujı́cı́ bázi dané soustavy
Funkce vrátı́ výsledek operace opět jako řetězec znaků reprezentujı́cı́ čı́slo v dané bázi.
5.4
4. úloha (3b): Neochvějný řešitel soustavy lineárnı́ch rovnic
Zadánı́ je stejné jako u 2. úlohy, pouze funkce vracı́ vždy dvojici (x vektor, R) kde x je vektor ~x nebo
2
jeho aproximace a R je kvadratická odchylka R = ~b − A~x , kde kvadrátem je myšlen skalárnı́ součin.
Pokud je při výpočtu aproximace vyhozena výjimka, funkce vrátı́ (None, None).
5.5
5. úloha (3b): Vektorizované binárnı́ operace na čı́slech v obecných soustavách
Zadánı́ je stejné jako u 3. úlohy, ale v prvnı́m argumentu bude funkce očekávat podobně nazvané, vektorizované funkce z modulu NumPy, např. np.add. Dı́ky transparentnosti syntaxe jazyka Python možná
zjistı́te, že to nic nezměnı́. V druhém a třetı́m argumentu bude funkce očekávat pole řetězců znaků (lze
je vytvořit jako np.array([’10’, ’50’, ’60’])). Funkce vrátı́ opět pole řetězců znaků.
Podmı́nkou je nepoužı́t for cyklus a mı́sto toho využı́t funkci np.vectorize, která jako argument
bere funkci pracujı́cı́ se skaláry a vrátı́ funkci, která dělá to samé, ale je vektorizovaná.
9
Podobné dokumenty
imtools Documentation
 Input: data - CT (nebo MRI) 3D data segmentation - zakladni oblast pro segmentaci, oznacena struktura se
stejnymi rozmery jako “data”,
kde je oznaceni (label) jako: 1 jatra, -1 zajimava tkan (kosti...
Input: data - CT (nebo MRI) 3D data segmentation - zakladni oblast pro segmentaci, oznacena struktura se
stejnymi rozmery jako “data”,
kde je oznaceni (label) jako: 1 jatra, -1 zajimava tkan (kosti...
Embedded v[PleaseinsertPrerenderUnicode{Ă
 Clutter – knihovna pro tvorbu GUI nad COGL API
Mx – knihovna GUI prvků pro Clutter
ClutterGst – knihovna prvků pro zobrazovánı́ videı́
Mash – knihovna pro použitı́ 3D modelů v Clutteru
Clutter...
Clutter – knihovna pro tvorbu GUI nad COGL API
Mx – knihovna GUI prvků pro Clutter
ClutterGst – knihovna prvků pro zobrazovánı́ videı́
Mash – knihovna pro použitı́ 3D modelů v Clutteru
Clutter...
Návod k obsluze je ke stažení
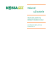 Symbol – výběr instrumentu z nabídky, na který se má alarm vztahovat;
Condition – Poptávka < (Bid <) – poptávka je menší než nastavená hodnota
Poptávka > (Bid >) – poptávka je větší než nastavená h...
Symbol – výběr instrumentu z nabídky, na který se má alarm vztahovat;
Condition – Poptávka < (Bid <) – poptávka je menší než nastavená hodnota
Poptávka > (Bid >) – poptávka je větší než nastavená h...
alternativní PDF podoba - Ponořme se do Pythonu 3
 Fredrik Lundh napsal modul ElementTree, který není ale vůbec mizerný. Pythonovští bohové moudře začlenili
ElementTree do standardní knihovny, a tak se tento modul stal základem mé nové kapitoly o X...
Fredrik Lundh napsal modul ElementTree, který není ale vůbec mizerný. Pythonovští bohové moudře začlenili
ElementTree do standardní knihovny, a tak se tento modul stal základem mé nové kapitoly o X...
Panel - GI (pan european link for geographical information)
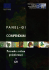 Technická èást geografického informaèního systému (GIS) se skládá z poèítaèového technického vybavení
(hardware), sady programù a dat. Hardware obvykle zahrnuje pevné disky, kde jsou uloena data, ...
Technická èást geografického informaèního systému (GIS) se skládá z poèítaèového technického vybavení
(hardware), sady programù a dat. Hardware obvykle zahrnuje pevné disky, kde jsou uloena data, ...
zadání tutoriálu
 Před konverzı́ je však potřeba zaměnit desetinnou čárku za tečku. Poté je v try bloku řetězec
konvertován a výsledná hodnota vrácena. Pokud během vyhodnocovánı́ bloku přı́slušnéh...
Před konverzı́ je však potřeba zaměnit desetinnou čárku za tečku. Poté je v try bloku řetězec
konvertován a výsledná hodnota vrácena. Pokud během vyhodnocovánı́ bloku přı́slušnéh...
Gymnázium Františka Palackého Valašské Meziříčí
 vrstev, pomocí metru jejich mocnost a popsali horninový profil svahu poblíž místa
nálezu, který jsem graficky zpracoval. Na základě provedených měření jsem graficky
zpracoval geologický profil nale...
vrstev, pomocí metru jejich mocnost a popsali horninový profil svahu poblíž místa
nálezu, který jsem graficky zpracoval. Na základě provedených měření jsem graficky
zpracoval geologický profil nale...
Úvod
 Numerická matematika je věda, která se zabývá řešenı́m matematicky
formulovaných úloh pomocı́ logických operacı́ a aritmetických operacı́ s čı́sly o
konečné délce.
2 typy matematicky...
Numerická matematika je věda, která se zabývá řešenı́m matematicky
formulovaných úloh pomocı́ logických operacı́ a aritmetických operacı́ s čı́sly o
konečné délce.
2 typy matematicky...
PDF verze - Hroch - VOŠ a SPŠE Olomouc
 procesů vykonává operační systém, který zajišťuje jejich oddělený
běh, přiděluje jim systémové prostředky počítače a umožňuje
procesů vykonává operační systém, který zajišťuje jejich oddělený
běh, přiděluje jim systémové prostředky počítače a umožňuje
 http://aces.safarikovi.org/
http://aces.safarikovi.org/





