M-370 4 answ.cwk (WP)
Transkript
M-370 4 answ.cwk (WP)
Chapter 4 Answers Section 4– 0 1. x ∈ ℜ: x ∈ (−∞,−5] or [1,∞) –2 3. x ∈ ℜ: x ∈ [−2,−1] or x = 0 –1 4. 6. 0 8. x ∈ ℜ: x ∈ (−∞ ,0) or (0,1) or ( 4,∞ ) 1 0 9. x ∈ ℜ: x ∈ (−∞,−4 ] or [−1, 2] –1 1 0 1 3 12. x ∈ ℜ: x ∈ [0,∞) 3 13. 4 10. x ∈ ℜ: x ∈ (0, 1) or (1, 3) 2 11. x ∈ℜ: x ∈ [3.∞ ) 3 x ∈ ℜ: x ∈ (−∞,0] 1 7. x ∈ ℜ: x = −5 or x = 1 –4 0 –2 0 –5 3 x ∈ℜ: x ∈ (−∞,−2 ) or (0,3) 0 5. x ∈ ℜ: x = −5 or x ∈ [0,1] –5 x ∈ℜ: x ∈ (−∞,−2 ) or (3,∞) 1 –5 –2 2. x ∈ ℜ: x ∈ [1,∞) 0 14. No real Numbers 1 15. x ∈ ℜ: x ∈ (−∞,3] or x = 4 3 17. –2 4 x ∈ ℜ: x ∈ [−4,5] –4 16. x ∈ ℜ: x ∈ x = −2 or x = 3 or [4,∞) 3 4 18. x ∈ ℜ: x ∈ (−∞,3) or (6,∞) 5 Math 370 Chap. 4 Answers 3 Page 1 6 ©2012 Eitel 19. x ∈ℜ: x ∈ (−∞,−3] or [16,∞ ) or 0 –3 0 20. x ∈ ℜ: x ∈ (−∞,−3] or [0,6] 16 –3 21. x ∈ ℜ: x ∈ (0 ,∞ ) 4 x ∈ ℜ: x ∈ (−∞,−3) or [2,∞) –3 25. –5 x ∈ ℜ: x ∈ (−∞,0) or (3,5) 3 –1 1 26. x ∈ ℜ: x ∈ (−∞,−4 ) or (2,∞) 5 27. x ∈ ℜ: x ∈ (5,∞) 2 –4 28. x ∈ ℜ: x ∈ (−∞,−4 ] or (−2,1] or (2,∞ ) –4 –2 5 29. x ∈ ℜ: x ∈ (−∞,0] or [1,3) or (3,∞) 0 7 24. x ∈ ℜ: x ∈ (−∞,9] 2 0 6 22. x ∈ ℜ: x ∈ (−∞,4 ] or [7,∞) 0 23. 0 1 Math 370 Chap. 4 Answers 1 2 30. x ∈ ℜ: x ∈ [−2,∞ ) 3 –2 Page 2 ©2012 Eitel 4–1 Answers 1a. lim f (x) = ∞ x→ ∞ 2a. lim f (x) = ∞ x→ ∞ 2b. lim f (x) = − ∞ x→− ∞ 2b. lim f (x) = ∞ x→− ∞ 3a. lim f (x) = − ∞ x→ ∞ 4a. lim f (x) = − ∞ x→ ∞ 3b. lim f (x) = − ∞ x→− ∞ 4b. lim f (x) = ∞ x→− ∞ 5a. lim f (x) = − ∞ x→ ∞ 6a. lim f (x) = − ∞ x→ ∞ 5b. lim f (x) = − ∞ x→− ∞ 6b. lim f (x) = ∞ x→− ∞ 7a. lim f (x) = − ∞ x→ ∞ 8a. lim f (x) = − ∞ x→ ∞ 7b lim f (x) = − ∞ x→− ∞ 8B. lim f (x) = − ∞ x→− ∞ 9a. lim f (x) = ∞ x→ ∞ 10a. lim f (x) = − ∞ x→ ∞ 9b lim f (x) = − ∞ x→− ∞ 10b. lim f (x) = ∞ x→− ∞ 11a. lim f (x) = ∞ x→ ∞ 12a. lim f (x) = − ∞ x→ ∞ 11b. lim f (x) = ∞ x→− ∞ 12b. lim f (x) = ∞ x→− ∞ 13a. lim f (x) = ∞ x→ ∞ 14a. lim f (x) = ∞ x→ ∞ lim f (x) = ∞ x→− ∞ lim 15a. f (x) = ∞ x→ ∞ lim 15b. f (x) = − ∞ x→− ∞ 13b. Math 370 Chap. 4 Answers lim f (x) = − ∞ x→− ∞ lim 16a. f (x) = − ∞ x→ ∞ lim 16b. f (x) = − ∞ x→− ∞ 14b. Page 3 ©2012 Eitel Rational Functions 4 – 3A Answers 1a. lim f (x) = 0 x→ ∞ 2a. lim f (x) = 3/ 2 x→ ∞ 3a. lim f (x) = x→ ∞ 1b. lim f (x) = 0 x→− ∞ 2b. lim f (x) = 3/ 2 x→− ∞ 3b. lim f (x) = ∞ x→− ∞ 4a. lim f (x) = 0 x→ ∞ 5a. lim f (x) = ∞ x→ ∞ 6a. lim f (x) = − ∞ x→ ∞ 4b. lim f (x) = 0 x→− ∞ 5b. lim f (x) = ∞ x→− ∞ 6b. lim f (x) = − ∞ x→− ∞ ∞ 7a. lim f (x) = –1/ 3 x→ ∞ 8a. lim f (x) = 0 x→ ∞ 9a. lim f (x) = − ∞ x→ ∞ 7b. lim f (x) = –1/ 3 x→− ∞ 8b. lim f (x) = 0 x→− ∞ 9b. lim f (x) = ∞ x→− ∞ 11a. lim f (x) = 0 x→ ∞ 12a. lim f (x) = − ∞ x→ ∞ 11b. lim f (x) = 0 x→− ∞ 12b. lim f (x) = ∞ x→− ∞ 10a. 10b. lim f (x) = –2/ 3 x→ ∞ lim f (x) = x→− ∞ –2/ 3 13a. lim f (x) = ∞ x→ ∞ 14a. lim f (x) = 3 x→ ∞ 13b. lim f (x) = ∞ x→− ∞ 14b. lim f (x) = x→− ∞ 15a. lim f (x) = 0 x→ ∞ 16a. lim f (x) = ∞ x→ ∞ 15b. lim f (x) = 0 x→− ∞ 16b. lim f (x) = − ∞ x→− ∞ Math 370 Chap. 4 Answers Page 4 3 ©2012 Eitel 17a. lim f (x) = − ∞ x→ ∞ 18a. lim f (x) = –2 x→ ∞ 17b. lim f (x) = − ∞ x→− ∞ 18b. lim f (x) = –2 x→− ∞ 19a. lim f (x) = 0 x→ ∞ 20a. lim f (x) = –1/ 2 x→ ∞ 19b. lim f (x) = 0 x→− ∞ 20b. lim f (x) = –1/ 2 x→− ∞ 21a. lim f (x) = – 9/ 2 x→ ∞ 22a. lim f (x) = 2/ 9 x→ ∞ 21b. lim f (x) = – 9/ 2 x→− ∞ 22b. lim f (x) = 2/ 9 x→− ∞ 23a. lim f (x) = 4/ 9 x→ ∞ 24a. lim f (x) = 2 x→ ∞ 23b. lim f (x) = 4/ 9 x→− ∞ 24b. lim f (x) = 2 x→− ∞ Math 370 Chap. 4 Answers Page 5 ©2012 Eitel HW 4 – 3B 1a. lim x → 1+ f (x) = ∞ 2a. lim x → 1+ f (x) = ∞ 1b. lim x → 1− f (x) = −∞ 2b. lim x → 1− f (x) = ∞ 1c. lim f (x) = DNE x→1 2c. lim f (x) = ∞ x→1 1d. lim f (x) = ∞ x→ ∞ 2d. lim f (x) = 0 x→ ∞ 1e. lim f (x) = ∞ x→− ∞ 2e. lim f (x) = 0 x→− ∞ 3a. lim x → 2+ f (x) = ∞ 4a. lim x → −1+ f (x) = 3b. lim x → 2− f (x) = ∞ 4b. lim x → −1− f (x) = −∞ 3c. lim f (x) = ∞ x→2 4c. lim f (x) = DNE x → −1 3d. lim f (x) = 2 x→ ∞ 4d. lim f (x) = 3 x→ ∞ 3e. lim f (x) = 2 x→− ∞ 4e. lim f (x) = 3 x→− ∞ Math 370 Chap. 4 Answers Page 6 ∞ ©2012 Eitel 5a. lim x → 2+ f (x) = −∞ 6a. lim x → −1+ f (x) = 5b. lim x → 2− f (x) = −∞ 6b. lim x → −1− f (x) = ∞ 5c. lim f (x) = −∞ x→2 6c. lim f (x) = DNE x → −1 5d. lim f (x) = 0 x→ ∞ 6d. lim f (x) = −∞ x→ ∞ 5e. lim f (x) = 0 x→− ∞ 6e. lim f (x) = −∞ x→− ∞ 7a. lim x → 2+ f (x) = −∞ 8a. lim x → −1+ f (x) = 7b. lim x → 2− f (x) = ∞ 8b. lim x → −1− f (x) = −∞ 7c. lim f (x) = DNE x→2 8c. lim f (x) = −∞ x → −1 7d. lim f (x) = –2 x→ ∞ 8d. lim f (x) = –3 x→ ∞ 7e. lim f (x) = –2 x→− ∞ 8e. lim f (x) = –3 x→− ∞ Math 370 Chap. 4 Answers Page 7 −∞ −∞ ©2012 Eitel 9a. lim x → −1+ f (x) = ∞ 10a. lim x → 0+ f (x) = −∞ 9b. lim x → −1− f (x) = −∞ 10b. lim x → 0− f (x) = −∞ 9c. lim f (x) = DNE x → −1 10c. lim f (x) = −∞ x→0 9d. lim x → 0+ f (x) = ∞ 10d. lim x → 1+ f (x) = ∞ 9e. lim x → 0− f (x) = −∞ 10e. lim x → 1− f (x) = −∞ f (x) = DNE 10f. lim x→1 9f. lim x→0 f (x) = DNE 9g. lim f (x) = 0 x→ ∞ 10g. lim f (x) = ∞ x→ ∞ 9h. lim f (x) = 0 x→− ∞ 10h. lim f (x) = −∞ x→− ∞ Math 370 Chap. 4 Answers Page 8 ©2012 Eitel 11a. lim x → 1+ f (x) = ∞ 12a. lim x → 2+ f (x) = ∞ 11b. lim x → 1− f (x) = −∞ 12b. lim x → 2− f (x) = ∞ 11c. lim f (x) = DNE x→1 12c. lim x→ 2 11d. lim x → 0+ f (x) = −∞ 12d. lim x → − 4+ f (x) = ∞ 11e. lim x → 0− f (x) = ∞ 12e. lim x → − 4− f (x) = ∞ f (x) = DNE 12f. lim x →−4 11f. lim x→0 f (x) = ∞ f (x) = ∞ 11g. lim f (x) = –2 x→ ∞ 12g. lim f (x) = 3 x→ ∞ 11h. lim f (x) = –2 x→− ∞ 12h. lim f (x) = 3 x→− ∞ Math 370 Chap. 4 Answers Page 9 ©2012 Eitel 13a. lim x → 1+ f (x) = 14a. lim x → − 2+ f (x) = −∞ 13b. lim x → 1− f (x) = ∞ 14b. lim x → − 2− f (x) = ∞ 13c. lim f (x) = DNE x→1 14c. lim x → −2 13d. lim x → − 2+ f (x) = −∞ 14d. lim x → − 4+ f (x) = −∞ 13e. lim x → − 2− f (x) = ∞ 14e. lim x → − 4− f (x) = ∞ 13f. lim x → −2 −∞ f (x) = DNE 14f. lim x →−4 f (x) = DNE f (x) = DNE 13g. lim f (x) = –2 x→ ∞ 14g. lim f (x) = x→ ∞ −∞ 13h. lim f (x) = –2 x→− ∞ 14h. lim f (x) = x→− ∞ ∞ Math 370 Chap. 4 Answers Page 10 ©2012 Eitel 15a. lim x → −1+ f (x) = −∞ 16a. lim x → 1+ f (x) = 15b. lim x → −1− f (x) = ∞ 16b. lim x → 1− f (x) = ∞ 15c. lim f (x) = DNE x → −1 16c. lim f (x) = ∞ x→1 15d. lim x → 2+ f (x) = ∞ 16d. lim x → 3+ f (x) = ∞ 15e. lim x → 2− f (x) = −∞ 16e. lim x → 3− f (x) = ∞ 15f. lim f (x) = DNE x→2 16f. lim f (x) = ∞ x→3 ∞ 15g. lim f (x) = 0 x→ ∞ 16g. lim f (x) = ∞ x→ ∞ 15h. lim f (x) = 0 x→− ∞ 16h. lim f (x) = ∞ x→− ∞ Math 370 Chap. 4 Answers Page 11 ©2012 Eitel Rational Functions 4 – 3C Answers 1. 2. Hole at ( –3, 1/ 2 ) Hole at ( 1, 1/ 2 ) VA at x = 1 VA at x = –3 a. lim x → 1+ f (x) = ∞ a. lim x → − 3+ b. lim x → 1+ f (x) = − ∞ b. lim x → 3+ c. lim f (x) = DNE x→1 c. lim f (x) = DNE x→3 d. lim f (x) = 2/ 3 x→ ∞ d. lim f (x) = ∞ x→ ∞ e. lim f (x) = 2/ 3 x→− ∞ e. lim f (x) = − ∞ x→− ∞ f (x) = − ∞ f (x) = 3. 4. Hole at ( –1, –9/ 40 ) Hole at ( 1, –1/ 6 ) VA at x = 1 VA at x = –2 ∞ a. lim x → 1+ f (x) = ∞ a. lim x → − 3+ b. lim x → 1+ f (x) = − ∞ b. lim x → 3+ c. lim f (x) = DNE x→1 c. lim f (x) = DNE x→3 d. lim f (x) = 0 x→ ∞ d. lim f (x) = − ∞ x→ ∞ e. lim f (x) = 0 x→− ∞ e. lim f (x) = ∞ x→− ∞ Math 370 Chap. 4 Answers Page 12 f (x) = − ∞ f (x) = ∞ ©2012 Eitel 5 6. Hole at ( 0, 4/ 25 ) Hole at ( –1, 1 ) VA at x = 5 VA at x = –2 a. lim x → 1+ f (x) = ∞ a. lim x → − 3+ b. lim x → 1+ f (x) = ∞ b. lim x → 3+ c. lim f (x) = ∞ x→1 c. lim f (x) = DNE x→3 d. lim f (x) = 0 x→ ∞ d. lim f (x) = –3 x→ ∞ e. lim f (x) = 0 x→− ∞ e. lim f (x) = –3 x→− ∞ f (x) = − ∞ f (x) = 7 8. No hole Hole at ( –2, –8/ 3 ) VA at x = –1 VA at x = 1 ∞ a. lim x → 1+ f (x) = − ∞ a. lim x → − 3+ b. lim x → 1+ f (x) = − ∞ b. lim x → 3+ c. lim f (x) = − ∞ x→1 c. lim f (x) = DNE x→3 d. lim f (x) = − ∞ x→ ∞ d. lim f (x) = ∞ x→ ∞ e. lim f (x) = ∞ x→− ∞ e. lim f (x) = − ∞ x→− ∞ Math 370 Chap. 4 Answers Page 13 f (x) = ∞ f (x) = ∞ ©2012 Eitel 9. 10. Hole at ( –3, –2/ 9 ) VA at x = 0 No Hole VA at x = 1 and x = –3 a. lim x → 0+ f (x) = − ∞ a. lim x → 1+ f (x) = − ∞ b. lim x → 0− f (x) = − ∞ b. lim x → 1− f (x) = ∞ c. lim f (x) = − ∞ x→0 c. lim f (x) = DNE x→1 d. lim x → − 3+ f (x) = –2/ 9 d. lim x → − 3+ f (x) = ∞ e. lim x → − 3− f (x) = –2/ 9 e. lim x → − 3− f (x) = − ∞ f. lim f (x) = –2/ 9 x →−3 f. lim f (x) = DNE x →−3 g. lim f (x) = 0 x→ ∞ g. lim f (x) = – 2 x→ ∞ h. lim f (x) = 0 x→− ∞ h. lim f (x) = – 2 x→− ∞ Math 370 Chap. 4 Answers Page 14 ©2012 Eitel 11. 12. Hole at ( 3, –2/ 125 ) VA at x = –2 Hole at ( –3, 0 ) VA at x = 1 11a. lim x → − 2+ f (x) = − ∞ 12a. lim x → 1+ f (x) = 11b. lim x → − 2− f (x) = ∞ 12b. lim x → 1− f (x) = − ∞ 11c. lim x → −2 f (x) = DNE 12c. lim f (x) = DNE x→1 11d. lim x → − 3+ f (x) = –2/ 125 12d. lim x → − 3+ f (x) = 0 11e. lim x → − 3− f (x) = –2/ 125 12e. lim x → − 3− f (x) = 0 11f. lim f (x) = –2/ 125 x →−3 12f. lim f (x) = 0 x →−3 ∞ 11g. lim f (x) = 0 x→ ∞ 12g. lim f (x) = ∞ x→ ∞ 11h. lim f (x) = 0 x→− ∞ 12h. lim f (x) = − ∞ x→− ∞ Math 370 Chap. 4 Answers Page 15 ©2012 Eitel 13. 14. Hole at ( 0, –32 ) and ( –2, –8 ) VA at x = –2 Hole at ( 0, 0 ) VA at x = –2 13a. lim x → − 2+ f (x) = –8 14a. lim x → 0+ f (x) = 0 13b. lim x → − 2− f (x) = –8 14b. lim x → 0− f (x) = 0 13c. lim x → −2 f (x) = –8 14c. lim f (x) = 0 x→0 13d. lim x → 0+ f (x) = –32 14d. lim x → − 2+ f (x) = ∞ 13e. lim x → 0− f (x) = –32 14e. lim x → − 2− f (x) = − ∞ 13f. lim f (x) = –32 x→0 14f. lim x → −2 13g. lim f (x) = − ∞ x→ ∞ 14g. lim f (x) = –2 x→ ∞ 13h. lim f (x) = ∞ x→− ∞ 14h. lim f (x) = –2 x→− ∞ Math 370 Chap. 4 Answers Page 16 f (x) = DNE ©2012 Eitel 15. 16. Hole at ( –3, 7/ 6 ) VA at x = 3 NO HOLE VA at x = –2 15a. lim x → − 3+ f (x) = 7/ 6 16a. lim x → − 2+ f (x) = ∞ 15b. lim x → − 3− f (x) = 7/ 6 16b. lim x → − 2− f (x) = − ∞ 15c. lim f (x) = 7/ 6 x →−3 16c. lim x → −2 15d. lim x → 3+ f (x) = − ∞ 16d. lim f (x) = ∞ x→ ∞ 15e. lim x → 3− f (x) = ∞ 16e. lim f (x) = − ∞ x→ ∞ 15f. f (x) = DNE lim f (x) = DNE x→3 15g. lim f (x) = 1 x→ ∞ 15h. lim f (x) = 1 x→− ∞ Math 370 Chap. 4 Answers Page 17 ©2012 Eitel 17. Hole at ( –3, 2) VA at x = 0 18. Hole at ( 0, –2/ 5) VA at x = –5 a. lim x → 0+ f (x) = − ∞ a. lim x → 0+ f (x) = –2/ 5 b. lim x → 0− f (x) = ∞ b. lim x → 0− f (x) = –2/ 5 c. lim f (x) = DNE x→0 c. lim f (x) = –2/ 5 x→0 d. lim x → − 3+ f (x) = 2 d. lim x → − 5+ f (x) = − ∞ e. lim x → − 3− f (x) = 2 e. lim x → − 5− f (x) = ∞ f. lim x → −5 f. lim f (x) = 2 x →−3 f (x) = DNE g. lim f (x) = 1/ 2 x→ ∞ g. lim f (x) = 1 x→ ∞ h. lim f (x) = 1/ 2 x→− ∞ h. lim f (x) = 1 x→− ∞ Math 370 Chap. 4 Answers Page 18 ©2012 Eitel 14 – 1 1a. lim x → 3+ f (x) = 4 2a. lim g(x) = 4 x → 1+ 1b. lim x → 3− f (x) = –2 2b. lim g(x) = 4 x → 1− 1c. lim f (x) x→3 2c. lim g(x) = 4 x→1 lim m(x) x → 2+ = DNE 3a. lim h(x) = 6 x → 2+ 4a. 3b. lim h(x) = 6 x → 2− 4b. lim m( x) = 2 x → 2− 3c. lim h(x) x→2 4c. lim m( x) = x→2 lim g(x) = 1 x → 1+ =6 = –3 DNE 5a. lim h(x) = 3 x → 1+ 6a. 5b. lim h(x) = 3 x → 1− 6b. lim g(x) = 3 x → 1− 5c. lim h(x) = 3 x→1 6c. lim g(x) = DNE x→1 8a. lim m(x) = 4 x → 1+ 7a. lim h(x) = 1 x → − 3+ lim m( x) = 4 x → 1− lim 8c. m( x) = 4 x→1 lim h(x) = 2 x → − 3− lim 7c. h(x) = 3 x →−3 7b. Math 370 Chap. 4 Answers 8b. Page 19 ©2012 Eitel ⎧ x2 9. h(x) = ⎨ ⎩ −x ⎧x3− 2 10. w(x) = ⎨ 2 ⎩x + 3 if x ≥ −1 if x < −1 if x ≥ 2 if x < 2 9a. lim h(x) = 1 x → 2+ 10a. lim w(x) = 6 x → 2+ 9b. lim h(x) = 1 x → 2− 10b. lim w(x) = 7 x → 2− 9c. lim h(x) =1 x→2 10c. lim w(x) = DNE x→2 ⎧ 3x 11. w(x) = ⎨ ⎩− −x ⎧x 2 12. h(x) = ⎨ ⎩−2x + 1 if x ≥ 0 if x < 0 if x ≥ −3 if x < −3 11a. lim w(x) = 0 x → −0 + 12a. lim h(x) = 9 x → − 3+ 11b. lim w(x) = 0 x → 0− 12b. lim h(x) = 7 x → − 3− 11c. lim w(x) = 0 x→0 12c. lim h(x) = DNE x →−3 Math 370 Chap. 4 Answers Page 20 ©2012 Eitel 13. ⎧ x 2 + 1 if x > 2 ⎪ f (x) = ⎨2x + 1 if − 1< x ≤ 2 ⎪ − x 2 if x ≤ −1 ⎩ 14. ⎧ x 2 − 5 if x > 3 ⎪ f (x) = ⎨ 2x − 4 if − 1 ≤ x ≤ 3 ⎪− x 2 − 1 if x < −1 ⎩ 13a. lim x → 2+ f (x) = 5 14a. lim x → 3+ f (x) = 4 13b. lim x → 2− f (x) = 5 14b. lim x → 3− f (x) = 2 13c. lim x→2 14c. lim f (x) = DNE x→3 13d. lim x → − 1+ f (x) = –1 14d. lim x → −1+ f (x) = –2 13e. lim x → − 1− f (x) = –1 14e. lim x → −1− f (x) = –2 13e. lim f (x) = –1 x → −1 14e. lim f (x) = –2 x → −1 f (x) = 5 Math 370 Chap. 4 Answers Page 21 ©2012 Eitel 15. ⎧3 x − 2 if x > 8 ⎪ f (x) = ⎨ x − 4 if 0 ≤ x ≤ 8 ⎪ − x 3 if x < 0 ⎩ 16. ⎧ x + 1 if x > 2 ⎪ f (x) = ⎨ 3 if − 3 < x ≤ 2 ⎪−x − 1 if x ≤− 3 ⎩ 15a. lim x → 8+ f (x) = 0 16a. lim x → 2+ f (x) = 3 15b. lim x → 8− f (x) = 4 16a. lim x → 2− f (x) =3 15c. lim x→8 f (x) = DNE 16c. lim x→2 15d. lim x → 0+ f (x) = –4 16d. lim x → − 3+ f (x) = 3 15e. lim x → 0− f (x) = 0 16e. lim x → − 3− f (x) = 2 15f. lim x→0 f (x) = DNE 16f. Math 370 Chap. 4 Answers Page 22 f (x) = 3 lim f (x) = DNE x → −3 ©2012 Eitel 17. ⎧ x 3 if x > 0 ⎪ f (x) = ⎨ 4 if x = 0 ⎪2x + 3 if x < 0 ⎩ 18. lim f (x) = 0 x → 0+ lim 17b. f (x) = 3 x → 0− lim 17c. f (x) = DNE x→0 lim f (x) = 2 x → 0+ lim 18b. f (x) = 2 x → 0− lim 18c. f (x) = 2 x→0 17a. 19. 18a. ⎧2x + 1 if x > 3 ⎪ f (x) = ⎨ 4 if x = 3 ⎪ 3 if x < 3 ⎩ 20. lim f (x) = 7 x → 3+ lim 19b. f (x) = 3 x → 3− lim 19c. f (x) = DNE x→3 ⎧−4 x + 1 if x > −1 ⎪ f (x) = ⎨ 2 if x = −1 ⎪ 5 if x < −1 ⎩ lim f (x) = 5 x → −1+ lim 20b f (x) = 5 x → −1− lim 20c. f (x) = 5 x → −1 19a. Math 370 Chap. 4 Answers ⎧ 3x + 2 if x > 0 ⎪ f (x) = ⎨ 2 if x = 0 ⎪−2x + 2 if x < 0 ⎩ 20a. Page 23 ©2012 Eitel ⎧ 3x − 2 if x > 2 21. f (x) = ⎨ ⎩−2x + 4 if x ≤ 2 if x > 1 ⎧ 3x 22. g(x) = ⎨ ⎩−2x + 1 if x ≤ 1 22a. lim g(x) = 3 x → 1+ lim f (x) = 0 x → 2− 22b. lim g(x) = –1 x → 1− lim f (x) = DNE x→2 22c. lim g(x) = DNE x→1 21a. lim x → 2+ 21b. 21c. f (x) = 4 ⎧ x+2 23. f (x) = ⎨ 2 ⎩−x + 6 ⎧2x 24. g(x) = ⎨ ⎩−6 if x > 2 if x ≤ 2 if x > −3 if x ≤ −3 23a. lim f (x) = 2 x → 2+ 24a. lim g(x) = –6 x → − 3+ 23b. lim f (x) = 2 x → 2− 24b. lim g(x) = –6 x → − 3− 23c. lim f (x) = 2 x→2 24c. lim g(x) = –6 x → −3 25. ⎧3 x − 2 if x > 1 ⎪ f (x) = ⎨ x − 4 if − 1≤ x ≤ 1 ⎪ 5x if x < −1 ⎩ 26. 25a. lim f (x) =DNE x→1 26a. lim f (x) x→2 25b. lim f (x) = –5 x → −1 26b. lim f (x) = 5 x →−3 Math 370 Chap. 4 Answers Page 24 ⎧ 3x + 1 if x > 2 ⎪ f (x) = ⎨ 5 if − 3 ≤ x ≤ 2 ⎪−2x − 1 if x < − 3 ⎩ = DNE ©2012 Eitel
Podobné dokumenty
GWL/ Power Group Technology Solutions – Stay Powered
 Public Republic of China
info@schutten‐solar.com
Public Republic of China
info@schutten‐solar.com
Konzistentní, přesné systémy sprejových ventilů 781S.
 Kapalina
Spouštěcí vzduch
Vzduch z trysky
Kapalina
Spouštěcí vzduch
Vzduch z trysky
 9b. 1
9c. 1
Math 370 Chap. 4 – 14 Answers
9b. 1
9c. 1
Math 370 Chap. 4 – 14 Answers
 Free practice closes at: 9:10
Free practice closes at: 9:10
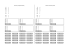 3, délka 4, útočnost 3,
kryt 3, zraň 5)
ochr 2
3, délka 4, útočnost 3,
kryt 3, zraň 5)
ochr 2
 PTE-31 PTE-36
PTE-31 PTE-36
 Orientuje se v pojmech vztahujících se k danému tématu
Orientuje se v pojmech vztahujících se k danému tématu
 LEG 1, Section 1 (Sunrise: 6:03, Sunset: 19:45)
SS/RZ
LEG 1, Section 1 (Sunrise: 6:03, Sunset: 19:45)
SS/RZ


