docOptické rozpoznávání znaků.
download 
Stížnost Podobné dokumenty
Populárně laděná prezentace o základech kvantové teorie ke
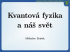• Když je částice ve stavu α |~r1i + β |~r2i, nemá smysl mluvit o její konkrétní poloze. Měření polohy ale vždy vede
k výsledku ~r1 nebo ~r2.
• α, β . . . komplexní čísla
– |α|2, |β|2 jsou úměrné p...
nemer volkswagen
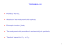Symbol např. (∂U/∂p)V označuje parciálnı́ derivaci U vzhledem k p při
konstantnı́m V a současně výraz indikuje, že uvažujeme U = U (p, V ).
Podobně výraz (∂U/∂p)Θ předpokládá, že U =...
pdf file
Součet 9 lze získat jako kombinaci výsledků 3 a 6 nebo 4 a 5. Součet 10 lze získat jako
kombinaci výsledků 5 a 5 nebo 4 a 6. Takže na první pohled by se mohlo zdát, že P (9) =
P (10). Ale počet vše...
2. kapitola.indd
umožňující připojení vodičů s průřezem
do 2x2,5 mm2 (2x14 AWG), tuhé nebo splétané,
s/bez koncových návlaček. Distribuce
potenciálu nevyžaduje přídavné koncové svorky
a tím tedy šetří čas a náklady...
Řešení V. série
Mnohasettisícitunový Ráma fungující na sluníčko by tedy nikam daleko nedoletěl.
Na konci úvodu jsme slíbili, že se ještě vrátíme k otázce realizovatelnosti zadaného Rá
mova způsobu cestování od Sl...
Text, který obsahuje poznámky k přednáškám
za nejpravděpodobnějšı́ (f). Lidé často seřadili tvrzenı́ takto: (f), (e), (d),
(a), (c), (b).
To je ovšem nesprávné. Pravděpodobnost (f) musı́ být vždy ≤ pravděpodobnost
(a) i než pr...