Kosinová veta pro ctyrúheln´ık (abstrakt)

příspěvek

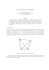Chceme-li se zabývat vztahy mezi prvky čtyřúhelnı́ka v euklidovské geometrii, je nejprve nutné shodnout se na použitém značenı́. Je-li dán čtyřúhelnı́k ABCD (viz obr. 1), je obvyklé z...

Prıklad 6. Zobrazte ve skutecné velikosti trojúhelnık ABC. A1 A2 B1

č. 9.třída 1 Barker Clive Abarat 2 Boyne John Chlapec v

19 Reeve Philip 20 Schmitt E.E. 21 Schmitt E.E. 22 Smith L.J. 23 Spiegelman Art 24 Stroud Jonathan 25 Terakowska Dorota 26 Viewegh Michal 27 Wyndham John

leták

= inkjet tiskárna - tisk 1 - 5 řádků, max. výška 12 mm, max. rychlost do 10,6 m/sek. APLINK UBS - tisk na savé i nesavé materiály (kartóny, fólie, atd.) = inkjet tiskárna s rozlišením tisku až 720 ...

Slon africký a indický

Hrají také důležitou roli v kultuře; například hinduistický bůh Ganéša má hlavu slona, jsou uváděny v Džátacích a v Kérale byli využíváni v průvodech ozdobeni slavnostním výstrojem.

Stieltjesu˚v integra´l (Kurzweilova teorie) Milan Tvrdy´

i Kurzweilův-Stieltjesův integrál. Dalšı́ podněty může čtenář najı́t také v monografiı́ch A. N. Kolmogorova a S. V. Fomina [17], E. Schechtera [46], W. Rudina [44] nebo skriptech J. Luke...