docMechanika těles - Statika (sbírka úloh)
download 
Stížnost Podobné dokumenty
Solid Edge
Pokud se připravuje vývoj stroje nebo zařízení, které je složeno z více podskupin,
první krok většinou spočívá na bedrech
projektanta. Ten musí připravit komplexní studii nového projektu. Tato prác...
1 POPISNÁ STATISTIKA
Lze přitom snadno ukázat, že souřadnicí tohoto těžiště je aritmetický průměr jednotlivých dat. Jinou přirozenou mírou polohy je medián neboli prostřední hodnota při
uspořádání dat podle velikosti. ...
Skořepinové konstrukce
Tlustostěnné skořepiny – tloušťka skořepiny h je srovnatelná s minimálním poloměrem křivosti plochy Rmin;
neplatí Kirchhoffova hypotéza tenkých desek – nelineární rozložení napětí po výšce
skořepin...
ČESKÉ VYSOKÉ UČENÍ TECHNICKÉ V PRAZE TEZE K
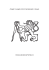Předložená disertační práce se zabývá vlivem ozáření na aktivační objem
pomocí rozboru výsledků instrumentovaných Charpyho zkoušek rázem v ohybu
s použitím inverzních metod a porovnáním s MKP. Výzk...
Skripta
se vyjadřuje pomocí tloušťky. V technické praxi se jedná o stěny, desky a skořepiny.
Stěna (wall) – Rovinná 2D konstrukce, která je zatížena a okrajové podmínky se
realizují v rovině stěny.
Deska (...
Stáhnout - mech - České vysoké učení technické v Praze
struktury. Materiálové charakteristiky jsou získány numerickou analýzou v prostředí MKP
aplikace Ansys tlakovým zatížením mikrostrukturálních modelů. Vnitřní struktura je modelována dvěma způsoby -...
Zatížení a spolehlivost
Řešení. V tomto případě bude mít zatížení obecný průběh
f (x) = A(x)ρg.
• Pokud použijeme k výpočtu výslednice přibližného výpočtu, rozdělíme
průběh zatížení na n intervalů 0 = x0 < x1 < . . . < xn...
