13. ZÁKLADNÍ TYPY DŮKAZŮ, VÝROKOVÁ LOGIKA

Logika tříd a relací

Logický čtverec Tradiční logický čtverec Logický čtverec je schéma, do kterého lze poměrně přehledně znázornit následující vztahy mezi tvrzeními: Kontradikce je vztah mezi dvěma tvrzeními s přesně ...

08 Příprava na 1_kompozici

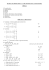a) Zapište množiny B, C intervalem b) Určete průnik intervalů B ∩ C c) Určete sjednocení intervalů B ∪ C

Balena 4000

Když Váš Douche WC stále ještě (dobře) nefunguje, zavolejte náš zákaznický servis.

Glynn Brothers Chemicals Prague spol. s r.o.

zavedené do kloubu, aplikujte Viscoseal do kloubního prostoru stlačením lahvičky. Tím se zajistí vymytí vyplachovacího roztoku. UPOZORNĚNÍ Musí být dodržena všechna doporučení pro intraartikulární ...

1 Integrál komplexní funkce – pokračování

kde C je kladně orientovaná kružnice |z − j| = 2. Vidíme, že integrovaná funkce má dvě singularity (t.j. body, kde není holomorfní). Jedna je v bodě 0 a druhá je v bodě 1. Singularita v bodě 0 je√o...

Propozice 472.7 KB - Klub českých turistů Queer

Avostalis del Pambio a Giovanni Lucchese, po nich Hans Tirol a Bonifác Wohlmut. Dvoupatrový letohrádek na unikátním půdorysu šesticípé hvězdy (díky kterému získal své jméno) patří do skupiny tzv. f...

Stáhnout - KoKoS - Gymnázium Mikuláše Koperníka

číslice jednotlivých součtů vždy 3. Proč? Pro k ≥ 5 už všechny hodnoty k! mají poslední číslici nula (vyskytuje se zde vždy součin 2 · 5), tudíž součet řady, kde n ≥ 5, bude vždy končit číslicí 3. ...

kryolipo