doczadání a řešení - Fyziklání online
download 
Stížnost Podobné dokumenty
Computing structural chemistry and biology
Síla působící na částici =
vektorový součet interakcí s ostatními
částicemi
F=m.a
zrychlení
FYKOS, XXVIII. ročník, 3. číslo
Bi sedí nedočkavě v pokoji na místě. V jednom okamžiku to nevydrží a rozpadne se. Zůstane nám z něj jádro thalia 205Tl a od něho letí pryč α částice. Jakou rychlostí
by se pohybovala α částice, pok...
Úvod em Zadá níIV .sé rie
v čočce jsou vzduchové mezery. Změřte, jakou část objemu sklenice tvoří tyto mezery. Měření opakujte i pro krystalový cukr.
Jako obvykle, pořádně popište, jak jste měření provedli, a nezapomeňte ho...
FYKOSí Fyziklání
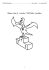zařízení proletět vícekrát a my máme možnost ji více urychlit. Na druhou stranu dochází při pohybu nabité částice po zakřivené dráze k vyzařování elektromagnetického záření. Výkon P tohoto tzv. syn...
zadání a řešení - Fyziklání online
Z definice Youngova modulu pružnosti víme, že se lano bude chovat jako pružinka tuhosti Eπr2 /h. Označme l délku, o kterou se lano během pádu protáhne. Celkově tedy lezcovo
těžiště kleslo o 2 (h − h...
FYKOS, XXVI.V.2 molekuly
vody L = 2,1 · 106 J·kg−1 a povrchové napětí vody (energie připadající na plošnou jednotku
povrchu kapaliny) α = 7,2 · 10−2 N·m−1 , odhadněte velikost jejích molekul.
Dominika se zamýšlela nad veli...
bezriziková výnosová míra – otevřený problém výnosového oceňování
na určité období, například na rok, a potřebuje se zajistit proti
nečekaným změnám úrokových měr. Jednou z možností je postup
založený na termínových úrokových mírách (angl. forward rates).
Termíno...
FYKOSí Fyziklání
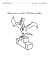Očekáváme vzorec ve tvaru R = Gα M β cγ /2. Například z Newtonova gravitačního zákona
vyjádříme [G] = m3 /(kg·s2 ). Pro kilogramy dostáváme podmínku α = β a pro sekundy zase 2α + γ = 0. Výsledek oč...
Řešení úloh Fykosího fyziklání 2008
2mπr
Ať je tedy částice kde chce a má jakoukoliv hmotnost, vždy získá stejný moment hybnosti
mv(r)r = (qLI)/(2π), který závisí jenom na náboji částice.
v(r) =
Sborník prezentací
c VŠB –Technická univerzita Ostrava, 17. Listopadu 15, 708 33 Ostrava – Poruba, ČR,
[email protected]
