Úvod em Zadá níIV .sé rie

zadání a řešení - Fyziklání online

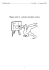Z definice Youngova modulu pružnosti víme, že se lano bude chovat jako pružinka tuhosti Eπr2 /h. Označme l délku, o kterou se lano během pádu protáhne. Celkově tedy lezcovo těžiště kleslo o 2 (h − h...

zadání a řešení - Fyziklání online

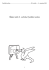oddělená úzkou mezerou. Zatímco v okolním prázdném prostoru existují vlny všech frekvencí, uvnitř dutiny mezi zrcadly existují jen takové vlny, jejichž vlnové délky odpovídají rezonancím v dutině. ...

Výsledky nejúspěšnějších řešitelů dle jednotlivých kategorií

Základní škola, Brno, Gajdošova 3, 615 00  Soukromá základní škola Lesná s.r.o., Janouškova 2, 613 00 Brno  CMCZŠ Lerchova 65, Brno 602 00  ZŠ a MŠ Raduň, Gudrichova 223, 747 61 Raduň  ZŠ Litultovi...

Bedřich Smetana

ztratil nejvěrnější ženu, na kterou po její smrti nepřestal vděčně vzpomínat a zaznamenal si do deníku své pocity (příloha č. 1). Byla pohřbena v hrobě na Olšanech, kde již ležela Bedřiška. Po její...

Eulerovy zásluhy o reformu goniometrie

Z obecného pohledu na goniometrii je nejvýraznější Eulerovou zásluhou, že různé (do té doby pouze numericky vyčíslované a tabulizované) trigonometrické hodnoty přetvořil ve funkce. Toto tvrzení vzh...

Seznam soutěžních prací a výsledky