Ukázka zápočtového testu č. 2 (jde o 2 varianty) 1) Nalezněte
Transkript
Ukázka zápočtového testu č. 2 (jde o 2 varianty) 1) Nalezněte
Ukázka zápočtového testu č. 2 (jde o 2 varianty) 1) Nalezněte všechny asymptoty grafu dané funkce, načrtněte části grafu v blízkosti asymptot. x2 + 3x + 2 x2 − 2x 3x2 + 2x + 1 b) f (x) = (x − 2)2 a) f (x) = 2) Nalezněte rovnici tečny ke grafu funkce f v bodě T . √ a) f (x) = 3 x2 + 4, T = [2, ?] 2 b) f (x) = x ex , T = [1, ?]. 3) Určete lokální extrémy funkce a) f (x) = x3 − 2x2 + x − 5 b) f (x) = cos2 2x. 4) Vypočítejte (1 − 2n)2 (3n + 5)3 (1 − 2n − n2 ) n→∞ (5n + 4)4 (2n3 − n2 + 1) cos x b) limπ π x→ 2 x − 2 a) lim Výsledky 1a) Svislá asymptota x = 2, zprava je limita +∞, zleva −∞, svislá asymptota x = 0, zprava je limita −∞, zleva +∞, vodorovná asymptota y = 1, v +∞ se funkce blíží k asymptotě shora, v −∞ zdola. 1b) Svislá asymptota x = 2, zprava i zleva je limita +∞; vodorovná asymptota y = 3, v +∞ se funkce blíží k asymptotě shora, v −∞ zdola. 2a) y − 2 = 1 3 (x − 2); T = [2, 2]. 2b) y = e (3x − 2); T = [1, e ]. 3a) Funkce má lokální maximum v bodě x = 1/3 a lokální minimum v bodě x = 1. 3b) Funkce má lokální minima v bodech x = (2k + 1) π4 a lokální maxima v x = k π2 , k ∈ Z. −54 , 4b) -1. 625 Upozornění: 4. příklad odpovídá pouze jedné variantě, tj. v testu budou 2 limity. 4a)
Podobné dokumenty
MBT1 – 4. týden
 5. a) maximum v bodě π/2, minimum v bodě −π/2, lokálnı́ extrémy nejsou,
b) lokálnı́ i globálnı́ maximum v bodě 1, minimum neexistuje lokálnı́ ani globálnı́,
c) lokálnı́ minimum v bodě 1,...
5. a) maximum v bodě π/2, minimum v bodě −π/2, lokálnı́ extrémy nejsou,
b) lokálnı́ i globálnı́ maximum v bodě 1, minimum neexistuje lokálnı́ ani globálnı́,
c) lokálnı́ minimum v bodě 1,...
str. 41, př. 1 Nakreslete grafy funkcí y=sinx, y=sin(x/2)
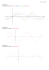 limπ tan ( 2 x ) .tan − x = limπ
π
limπ tan ( 2 x ) .tan − x = limπ
π
Matematika 1 - Sdružení TurnovFree.net
 svislé asymptoty, které mají rovnici x = a, pro nějaké a ∈ R;
vodorovné asymptoty, které mají rovnici y = b, pro nějaké b ∈ R;
šikmé asymptoty, které mají rovnici y = kx + q, pro nějaká k , 0 a
...
svislé asymptoty, které mají rovnici x = a, pro nějaké a ∈ R;
vodorovné asymptoty, které mají rovnici y = b, pro nějaké b ∈ R;
šikmé asymptoty, které mají rovnici y = kx + q, pro nějaká k , 0 a
...
Studijní text - MATEMATIKA online
 nekonečně malých veličin”. Ve zmíněné knize je poprvé uveřejněno tvrzení, které je v současné době známé
jako l’Hospitalovo pravidlo pro výpočet limit. Je paradoxní, že autorem tohoto tvrzení je l’...
nekonečně malých veličin”. Ve zmíněné knize je poprvé uveřejněno tvrzení, které je v současné době známé
jako l’Hospitalovo pravidlo pro výpočet limit. Je paradoxní, že autorem tohoto tvrzení je l’...