docdoprovodný text
download 
Stížnost Podobné dokumenty
IAJCE Přednáška č. 10 1 každému znaku je nutné přiřadit
o Vrací podřetězec od pozice start
Instanční metoda string Substring(int startIndex, int N)
o Vrací podřetězec od pozice start délky N znaků
o Příklad:
string osloveni = "Mile deti!";
string koho =...
22 Riemannova metrika a obsah plochy
Necht’ plocha Γ je určena rovnicemi x = s, y = t a z = es a křivka γ na této ploše je
definována rovnicemi x = cos τ a y = sin τ , kde τ ∈ h0, 2πi.
Pak délka této křivky na dané ploše je
Masarykova Univerzita Plošná fotometrie eliptických galaxi´ı
Obě spirálnı́ skupiny jsou členěny na tři poddruhy podle poměru jasnosti galaktické výdutě
a disku a podle mı́ry zatočenı́ (rozevřenı́) spirálnı́ch ramen (k označenı́ se přidávajı́ m...
Matematicka´ poha´dka
vylézá derivace ze svého doupěte. Zahlédla bojovnı́ka a vrhá
se na něj. Arcus však neotálı́ a útočı́ svým integračnı́m mečem,
exponenciálnı́m štı́tem kryje každý pokus o zderivova...
Řešení V. série
kládejme (pro spor) různé energie ve dvou různých bodech povrchu. Na křivce parametrizované
t, která body spojuje, je energie spojitou funkcí t a podle věty o střední hodnotě zde existuje
bod s nen...
Počítačová Tomografie Werth
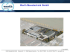Počítačová tomografie integrovaná do multisenzorového souřadnicového měřicího stroje
- Měření velkých dílců a komponentů s vysokou hustotou VT-A-7-3-0328_E
nemer volkswagen
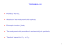X · rot X = X · (X × y) = 0
Protože X ̸= 0 a rot X =
̸ 0 (nesplněni integrability) předchozı́ rovnice je
nutnou podmı́nkou pro existenci µ. (t.j., existence µ ⇒ X · rot X = 0 )
Na druhé straně...
Spektrální a korelační analýza
• používá se pro detekci rytmů, které jsou společné mezi
dvěma signály (v případě EEG v obou hemisférách)
• CCF má stejnou frekvenci jako složka, která je
přítomna v obou kanálech