doc22 Riemannova metrika a obsah plochy
download 
Stížnost Podobné dokumenty
21 Plochy
je tedy lineárnı́ kombinacı́ těchto dvou vektorů
γ1 0 Γ~0s + γ2 0 Γ~0t .
Tečný vektor ke křivce je tečným vektorem i k ploše, křivka γ(t) byla vybrána libovolně,
pouze pricházı́ bodem ...
Matematicka´ poha´dka
Nejsem přı́liš bohatý, mám pouze kompaktnı́ definičnı́ obor D 0 = h−1, 1i. Dejte mi vaši dceru, krásnou Sinus,
a budu spokojen.“ Dostal tedy princeznu a zplodil s nı́ roztomilou identitu, by...
23 Neorientovaný plošný integrál
Vypočtěte integrál Γ z dS, kde Γ je stejně jako v přı́kladu 22.12 část šroubového konoidu
x = t cos s, y = t sin s, z = s pro 0 ≤ t ≤ 1 a 0 ≤ s ≤ 2π.
MA2
doprovodný text
Metoda simplexů zavádı́ (n+1) n–tice, vektory, odhadů parametrů a vytvářı́ z nich v prostoru
parametrů těleso o (n+1)–vrcholech – simplex. V přı́padě lineárnı́ regrese (2 hledané parame...
Stáhnout
3.3 Vlastnosti šroubovice
Věta 9. Tečny šroubovice svı́rajı́ konstantnı́ úhel s rovinou kolmou k ose šroubovice, resp.
s osou šroubového pohybu. Řı́káme, že šroubovice je křivka konsta...
nemer volkswagen
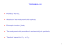nutnou podmı́nkou pro existenci µ. (t.j., existence µ ⇒ X · rot X = 0 )
Na druhé straně, hodnost sustavy rovnic pro µ je 2. Podmı́nka X·rot X = 0
zajišt’uje, že hodnost rozšı́řené matice je ...
F1 - Natura
Pravidla kvantové mechaniky pro svoji formulaci vyžadujı́ koncept času. Časová souřadnice určuje
volbu kanonické polohy a hybnosti, normalizaci vlnové funkce a samozřejmě evoluci kvantov...
8 Urcitý integrál, krivkový integrál a Cauchyovy integráln´ı vety
8.2 Věta (vlastnosti primitivnı́ch funkcı́).
i) Je-li F primitivnı́ funkce k f na Ω, potom také F + c je primitivnı́ funkcı́ k f na Ω pro
libovolné c ∈ C.
ii) Jsou-li F, G primitivnı́ funkce k f...
ACPI a Software Suspend
Při bootu se stav zase obnoví
Nepotřebuje podporu podporu BIOSu (ani ACPI),
pro hardware je to normální vypnutí a zapnutí
Užitečné pro notebooky, ale i pro desktop:
systém naběhne rychleji, nemusít...
