l b b l • rozsah slyšitelných frekvencí: 1.2 – 120 kHz • velryba beluga

kancelářské boxy

přední zešikmení odkládací plochy pro zadržení uložených dokumentů, pevný materiál zajišťující stabilitu při stohování odkladačů, kompatibilní s univerzálním nástavcem pro zvýšení kapacity odkládán...

Pasivní lineární obvody 1. a 2. řádu (RC, RL a RLC články)

doc. Ing. Jiří Sedláček, CSc. doc. Ing. Miloslav Steinbauer, Ph.D. doc. Ing. Petr Drexler, Ph.D. UTEE FEKT VUT v Brně

Teoretické otázky PROFANT 2007

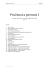 zx τ zy σ z  Napjatost v bodě tělesa je jednoznačně určena tenzorem napětí Tσ.

7/4.1 typynapjatostiatransf ormacenapjatosti

pouze jedno normálové napětí nenulové a všechna ostatní napětí jsou rovna nule. V tomto případě hovoříme o jednoosé napjatosti nebo někdy také o napjatosti přímkové, protože všechna napětí mají smě...

Skořepinové konstrukce

skořepiny, velice složité řešení blízké tlustým deskám Tenkostěnné skořepiny - velmi malá tloušťka stěny ve srovnání s minimálním poloměrem křivosti střednicové plochy; lze zanedbat vliv smykových ...

VT 4120 - Calibra CZ, s.r.o.

zabezpečte, aby nedocházelo k silovému namáhání kabelů před začátkem čištění nebo údržby zařízení vždy odpojte od síťového napájení zařízení vypněte a odpojte od síťového napájení, pokud jsou poško...

Popis předmětu

Soubor_Katalog kategorie

7 Lineární elasticita