HEMICKÁ TERMODYNAMIKA

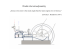
3. CHEMICKÁ TERMODYNAMIKA
Jak název naznačuje, vznikla termodynamika původně jako výsledek úvah o vztahu mezi teplem a
prací, o možnostech využití a kvantitativního určení přeměny tepla v práci. Dnes je definována
obecněji; pojednává o vzájemných přeměnách různých druhů energie, o směru fyzikálních a chemických dějů a o rovnováze.
Jako celek je termodynamika velmi rozsáhlá disciplína a svými principy a aplikacemi zasahuje
do řady technických vědních oborů; může např. poskytnout informace
o maximální účinnosti tepelných strojů,
o tom, zda uvažovaná reakce může probíhat samovolně,
jakého výtěžku je možno za daných podmínek dosáhnout,
jak je možno stanovit meze přesnosti určitého analytického postupu,
o určení podmínek nutných k zamezení nežádoucích vedlejších reakcí
o základech technických metod dělení reakčních produktů (destilace, extrakce, krystalizace)
o možnosti uplatnění v biologických vědách (bioenergetika, biotermodynamika).
Živé organizmy využívají energii uloženou v molekulách živin nebo zachycenou ze slunečního záření pro výstavbu
svých součástí a pro plnění všech životních funkcí, jako jsou pohyb, mechanická práce, aktivní transport apod.
Charakter klasické termodynamiky
 Je založena na několika základních postulátech, formulovaných axiomaticky, které nelze dokázat, ani vyvrátit. Lze je matematicky vyjádřit a je logickou cestou z nich odvozen aparát, který
dovoluje řešit problémy spojené s energetickými změnami. K tomu používá řadu pojmů zavedených definicí, např.
termodynamické funkce vnitřní energie U, entalpie H, entropie S,
Gibbsova energie G a Helmholtzova energie F,
které
jsou stavovými veličinami a souvisejí známým způsobem s měřitelnými veličinami p, T, n, ...
na rozdíl od základních stavových veličin, které jsou přímo měřitelné, definují termodynamické
vztahy pouze změny termodynamických funkcí (infinitezimální dX nebo konečné X)
To, že klasická termodynamika dovede vyjadřovat pouze změny termodynamických funkcí a není
schopna určit nulu pro udávání absolutních hodnot těchto veličin, není pro nás ve skutečnosti žádným
handicapem. Náš zájem je obecně soustředěn na chemické a fyzikální přeměny, a pak může být každý
stav volen za referenční bod pro vyjadřování termodynamických funkcí. Zvolíme si proto určitý, přesně definovaný referenční stav (tzv. standardní stav), k němuž termodynamické funkce vztahujeme.
Případ je podobný jako při udávání výšky hor. Měříme ji od hladiny moře, to znamená, že hladina moře je standardním stavem, k němuž vztahujeme všechna výšková měření.
Termodynamické veličiny systému, jehož součásti jsou ve standardním stavu, nazýváme pak standardní veličiny a značíme indexem , např. U. S, G. Standardní stav volíme, ale musíme jej přesně definovat; volba se řídí podle povahy systému a daného problému tak, aby jeho řešení bylo co nejjednodušší. Nejčastěji za standardní stav volíme
u plynů: plyn v ideálním stavu za tlaku 101,325 kPa při udané teplotě,
u kapalin: kapalinu za tlaku 101,325 kPa při udané teplotě,
u tuhých látek: nejstálejší tuhou modifikaci za tlaku 101,325 kPa při udané teplotě,
u roztoků: roztok dané látky o aktivitě rovné 1 (přibližně tedy o koncentraci 1 mol dm–3) za tlaku
10l,325 kPa při udané teplotě.
ani změny termodynamických veličin nejsou přímo měřitelné, počítají se pomocí měřitelných
veličin, jako jsou tepelné kapacity, reakční tepla, rovnovážné konstanty, elektromotorická napětí galvanických článků, tlaků nasycených par atd.
 Veličiny definuje pro idealizované děje s látkami ideálních vlastností; dostane jednoduché a přehledné vztahy, do kterých pro reálné systémy zavádí vhodně definované veličiny, vyjadřující odchylky od ideality.
 Je věda popisná – popisuje systém makroskopickými vlastnostmi, vyjadřuje vztahy mezi nimi,
ale nevykládá příčiny svých výsledků; neuvažuje o struktuře hmotné náplně soustavy – její závěChemická termodynamika
14
ry nejsou vázány na představy o stavbě hmoty a jiné teorie (její stavba se nezmění, vyskytne-li se
v atomistice nějaký nový pokrok). Odvozené vztahy však platí pouze pro makroskopické procesy. Nevypovídá nic o způsobu, jakým děje probíhají; čas jako proměnná zde nevystupuje.
 Termodynamické úvahy lze použít jen pro systémy s dostatečně velkým počtem částic, nikoliv
pro jednotlivé atomy nebo molekuly.
POSTULÁT O EXISTENCI TERMODYNAMICKÉ ROVNOVÁHY
Ze zkušenosti je známo, že každý děj je podmíněn existencí hybné síly, po jejímž vyčerpání přejde
systém do stavu rovnováhy, v němž se jeho vlastnosti nemění s časem. Je tedy např. rovnováha
mechanická - výslednice všech sil působících na systém je nulová
tepelná
- všechny části systému jsou tepelně vyrovnány
koncentrační - ve všech částech každé fáze systému jsou stejné koncentrace složek, složení různých fází se však zpravidla liší
chemická
- nemění se počet a kvalita složek, v systému neprobíhá žádná chemická reakce
fázová
- nemění se skupenství
termodynamická - s časem se nemění chemické složení ani termodynamické funkce
Pojem rovnováhy si objasníme na jednoduchém modelu. Na obr. 3-1 jsou znázorněny tři různé polohy předmětu
(láhve, kuželky) na horizontální desce. Potenciální energie kuželky je mgh (h je výška těžiště nad základnou).
V poloze (a) má kuželka vyšší energii než v poloze (c).
Tendence spadnout do polohy (c) se však nemůže projevit, dokud kuželka nedostane patřičný impulz (např. náraz
h
kulečníkové koule), čímž se dostane do přechodné polohy
(b). Na spodní části obr. 3-1 je graficky znázorněna změna
(a)
(b)
(c)
potenciální energie kuželky s úhlem náklonu . Je vidět, že
chceme-li kuželku porazit, musíme nejprve zvětšit její
mg h
energii tak, aby se dostala přes energetický val, který dělí
E*
rovnovážnou polohu (a) od rovnovážné polohy (c). Tento
rozdíl energií se nazývá aktivační energie E*.
Obr 3-1
0
a
1
b
90o
c
Rovnovážná poloha (a) metastabilní,
(b) nestabilní a (c) stabilní
Tento příklad ilustruje důležité aspekty popisu rovnovážného stavu: poloha (c) je stav o nejnižší možné energii,
které soustava může dosáhnout. Říkáme, že systém je ve stabilní rovnováze. Poloha (a) je stabilní vůči malým impulzům; přesáhne-li však dodaná energie určitou mez (E*), přechází systém do stavu (c) – hovoříme o metastabilní rovnováze. Polohy (b), v níž je energie maximální, může být sice dosaženo pečlivým vyvážením, ale nepatrný
impulz v jednom nebo druhém směru způsobí, že se kuželka převrátí do jednoho nebo druhého energetického minima. Tento stav se nazývá nestabilní rovnováha.
NULTÁ VĚTA TERMODYNAMICKÁ
Nultá věta termodynamická postuluje existenci teploty. Jsou-li dva systémy v tepelné rovnováze, tj.
při kontaktu nedochází k tepelnému toku z jednoho systému do druhého, mají oba systémy stejnou
teplotu. Má-li systém A stejnou teplotu jako systém B a systém B stejnou teplotu jako systém C,
pak také systém A má stejnou teplotu jako systém C. Chceme-li se tedy přesvědčit, mají-li dva systémy stejnou teplotu, nemusíme je k sobě přikládat, ale stačí použít teploměr – systém B.
PRVNÍ VĚTA TERMODYNAMICKÁ
První věta termodynamická je rozšířením principu zachování mechanické energie. Důvodem bylo
poznání, že vynaložením práce se může vyvinout teplo. Práce i teplo jsou formy převodu energie
(nikoliv tedy formy energie), které mají význam pouze ve spojení s převodem energie mezi soustavami. Nemůžeme tedy mluvit o teple nebo práci soustavy, ale můžeme mluvit o energii soustavy jako schopnosti měnit
daný stav systému.
První kvantitativní experimenty s přeměnou práce v teplo prováděl Benjamin Thompson, rodák z Woburnu
Chemická termodynamika
15
v Massachusetts, pozdější hrabě Rumford Svaté říše římské.
Když ho totiž vévoda bavorský pověřil dohledem na vrtání
dělových hlavní v mnichovském arzenálu, velice ho zaujala
skutečnost, že se při této činnosti vyvíjí teplo. Vyslovil názor
(1798), že toto teplo má zřejmé původ ve vynaložené mechanické energii, a dokázal odhadnout, jak velké teplo by se tímto způsobem vyvinulo, kdyby byla vynaložena práce, kterou vykoná kůň za jednu hodinu;
odhadl tak tzv. tepelný ekvivalent mechanické práce (jeho hodnota - vyjádřena v později
užívaných jednotkách tepla a práce - činila 0,183 cal/J). Jeho současníci však podrobili tyto
experimenty ostré kritice a tvrdili, že teplo se vyvíjí proto, že kov má v podobě jemných pilin menší specifickou tepelnou kapacitu než v kompaktním kuse. Rumford odpověděl novým
pokusem; použil tupého vrtáku a ukázal, že se vyvinulo stejně velké teplo, přestože se nevytvořily téměř žádné piliny. Tehdy zastánci kalorické hypotézy přišli s tvrzením, že teplo má původ v působení vzduchu
na nově vytvářený povrch kovu. Rumfordovu teorii ovšem značně podpořil roku 1799 Humhry Davy. Na základě pokusu, při němž se působením hodinového strojku o sebe třely dva kusy ledu ve vakuu, totiž ukázal, že i za nepřítomnosti
vzduchu led rychle taje, což znamená, že potřebné skupenské teplo bylo získáno z dodané mechanické práce. Přes to
všechno však tehdejší doba ještě nebyla natolik vědecky vyspělá, aby mohla mechanickou teorii tepla přijmout. Situace
se začala měnit až tehdy, když Dalton a ostatní svými pracemi položili základy atomové teorie látek, a tím začali postupně vytvářet předpoklady pro chápání tepla na základě pohybu molekul.
Nejpozději kolem roku 1840 byl již zákon zachování energie obecně přijat pro mechanické soustavy, vzájemná
přeměna práce v teplo se považovala za prokázanou a všeobecně se uznávalo, že teplo je prostě forma pohybu nejmenších částeček, z nichž se látka skládá. Avšak takové zevšeobecnění zákona zachování energie, které by zahrnovalo také
tepelné změny, v té době ještě jasně zformulováno nebylo.
V těchto souvislostech si nyní všimněme práce, kterou na tomto poli vykonal Julius Robert Mayer, jedna z nejpodivuhodnějších osobnosti v dějinách přírodních věd. Narodil se
roku 1814 jako syn lékárníka v Heilbronnu. Nebyl sice nijak vynikající student, avšak přesto
se v roce 1832 dal zapsat ke studiu lékařství na univerzitě v Tübingenu a jako žák Gmelinův
tam získal dobré základní vědomosti z chemie. V roce 1838 dosáhl doktorátu na základě
krátké disertace pojednávající o vlivu santoninu na škrkavky u dětí. Na celém období jeho
univerzitních studií nebylo nic, co by nasvědčovalo tomu, že jde o muže, který jednou tak velikou měrou přispěje k rozvoji přírodovědy.
Protože si přál poznat svět, přijal místo lodního lékaře na trojstěžníku Java a na jeho palubě vyplul v únoru 1840 z Rotterdamu. Dlouhou cestu strávil v blažené nečinnosti, kolébán
konejšivými příbřežními vánky. Podle Ostwaldova názoru se tím v něm nahromadila ohromná duševní energie, která se pak brzy po přistání měla naráz uvolnit. Podle vlastního Mayerova doznání se tok jeho myšlenek začal prudce odvíjet od okamžiku, kdy
v surabajském přístavu musel několika námořníkům pustit žilou. Krev
tekoucí ze žíly byla totiž tak jasně červená, že si v prvním okamžiku
myslel, že omylem otevřel tepnu. Od místních lékařů se však dověděl, že
tato světlá barva žitní krve je v tropech zcela typická, neboť na zachování potřebné teploty těla se tam spotřebuje daleko méně kyslíku než v krajích chladnějších. Kolem této základní myšlenky začal Mayer rozvíjet
své další úvahy. Jelikož živočišné teplo vzniká oxidací živin, nabízela se
otázka, co vlastně nastává, když se tělo nejen zahřívá na potřebnou teplotu, ale navíc ještě koná práci. Ukazovalo se, že z téhož množství potravy bylo možno získat někdy více a jindy méně tepla. Připustíme-li ovšem, že z dané potravy lze získat zcela určitý,
vždy stejný celkový výtěžek energie, nezbývá než připustit, že práce a teplo jsou veličiny téhož druhu, z nichž jedna
může přecházet v druhou. V důsledku spálení téhož množství potravy může sice tělo živočicha produkovat teplo a práci
v nejrůznějším vzájemném poměru, avšak součet obou musí vždy zůstat konstantní. Své dny na lodi trávil nyní Mayer v
horečné práci na své teorii. Změnil se v člověka posedlého jedinou velkou myšlenkou, jíž neváhal zasvětit svůj život.
Ve skutečnosti ovšem Mayerovi nebylo vůbec jasno, jak tomu je s rozdíly mezi pojmy síla, hybnost, práce a energie,
a proto také první sdělení, které o svých poznatcích sepsal, nebylo vědeckým redaktorem časopisu, jemuž je pak zaslal,
vůbec uveřejněno. Poggendorf prostě celou věc odložil a ani neodpovídal na Mayerovy dopisy. Do začátku roku 1842 však již Mayer své myšlenky propracoval do té
míry, že mohl položit rovnítko mezi teplo na jedné straně a kinetickou a potenciální energii na straně druhé. A v březnu 1842 již Liebig přijímá jeho sdělení k uveřejnění v časopise Annalen der Chemie und Pharmazie.
Přestože Mayer byl filosofickým otcem první věty termodynamiky, byly to teprve Joulovy nádherně přesné pokusy, které tuto větu postavily na pevné experimentální a induktivní základy. James Prescott Joule se narodil r. 1818 blízko
Manchestru jako syn zámožného majitele pivovaru. Na studiích byl žákem Johna
Daltona. Již jako dvacetiletý začal v laboratoři, kterou jeho otec zřídil při pivovaru,
provádět samostatné výzkumy. Ani v pozdějších letech, kdy se s úspěchem věnoChemická termodynamika
16
val vedení pivovaru, neustal ve své rozsáhlé práci na poli experimentální chemie a fyziky. V r. 1840 uveřejnil práci o
tepelných účincích elektrického proudu. Jestliže proud protéká kovovým vodičem, pak teplo, které se při tom za danou
dobu vyvine, je přímo úměrné odporu vodiče násobenému čtvercem intenzity elektrického proudu. Toto teplo lze považovat za teplo tření, vznikající pohybem částic přenášejících proud vodičem. Pak se Joule v dlouhé řadě neobyčejně
pečlivých experimentů věnoval proměřování přeměny práce v teplo různými způsoby, jako je elektrický ohřev, stlačování plynů, protlačování kapalin jemnými kapilárami a otáčení lopatkovým kolem ve vodě a ve rtuti. Po zahrnutí všech
korekcí dospěl k závěru, že 1 cal = 4,154 J (dnes 1 cal = 4,184 J).
Mayerovy filosofické argumenty a Joulovy experimentální práce vedly
k definitivnímu přijetí principu zachování energie. Hermann von Helmholtz
(1847) dal tomuto principu důkladnější matematický základ ve své práci „O
zachování síly“, v níž také zachování energie jasně prohlásil za obecně platný princip a za jeden ze základních zákonů, který lze aplikovat na všechny
přírodní jevy. Každé soustavě připsal určitý obsah energie. Tato energie je
dána uspořádáním jejich nejmenších částic a jejich pohybem; je skryta v interakcích, uspořádání a pohybech stavebních jednotek látek. Je tedy funkcí
jen těch veličin, které nejsou v žádném vztahu k okolí. Abychom to zdůraznili, nazýváme takovouto energii soustavy vnitřní energie.
Míníme jí tedy např. u plynu translační kinetickou energii pohybujících se molekul, k ní se
přičítá rotační energie atomů v molekule, vibrace atomů atd. U látek pevných je to převážně energie molekul oscilujících
kolem jejich rovnovážných poloh v krystalových mřížkách, rotační a vibrační energie atomů atd. K tomu přistupuje ještě
potenciální energie elektronů a atomů, určená jejich uspořádáním v molekule: pokud se v systému vyskytuje nějaký druh
záření, tedy i zářivá energie atd.
Vnitřní energii budeme označovat symbolem U. Je to stavová veličina, neboť charakterizuje stav
soustavy a závisí pouze na něm a ne na předchozím osudu systému. Přechod soustavy z jednoho
stavu do druhého bude tedy charakterizován příslušnou změnou U, která bude záviset pouze na
konečném a výchozím stavu soustavy a ve shodě se zkušeností bude stejná, ať ke změně stavu došlo
jakýmkoli způsobem. Kdyby se totiž ukázalo, že při některém způsobu převedení dané soustavy z
výchozího do konečného stavu by se spotřebovalo méně energie než při jiných cestách, znamenalo
by to, že by bylo možno vhodným sledem cest získávat z ničeho energii, což však zcela odporuje
veškerým zkušenostem.
Při změnách stavu soustavy látek nastává tedy změna obsahu vnitřní energie; termodynamika nesleduje, jakým mechanismem ke změně došlo, ale bere do počtu součet všech energií, jež se na
změně energetického obsahu soustavy podílely. Tuto změnu si můžeme rozdělit na část tepelnou a
netepelnou; zkušenosti totiž učí, že se obě části dají pozorováním rozlišit přesto, že jsou fyzikálně
ekvivalentní.
Důvod, proč stavíme právě tepelnou energii proti všem ostatním druhům energie, je v tom, že
každou energii dovedeme beze zbytku přeměnit v teplo, kdežto teplo můžeme přeměnit
v netepelnou energii jenom částečně. Tuto netepelnou formu energie nazýváme prací a označujeme
W; je jí především mechanická práce, kterou soustava koná tím, že přemáhá vnější síly na ni působící (–W), nebo kterou na soustavu vynakládáme (+W). Netepelnou formou energie může být ovšem
též např. energie elektrická, magnetická, zářivá, povrchová apod. Tepelnou část energie označíme
Q; v duchu zavedené konvence bude +Q teplo, které soustava přecházející ze stavu A do B přijala
ze svého okolí. a znaménko minus bude znamenat, že soustava teplo naopak do okolí vydala.
Změnu vnitřní energie systému při přechodu z výchozího stavu A do konečného stavu B,
U = UB – UA, pak tedy můžeme vyjádřit jako součet množství tepla Q a práce W přijatých systémem z okolí při tomto přechodu:
U = Q + W , pro infinitezimální změny dU = đQ + đW
(3.1)
Vztahem (3.1) je matematicky formulována první věta termodynamická (symbol đ označuje neúplný diferenciál, neboť na rozdíl od vnitřní energie, tepla a práce nejsou stavové funkce).
Ke změně vnitřní energie systému může tedy docházet pouze interakcí s okolím (tedy u uzavřených a otevřených
systémů, zatímco u izolovaného systému zůstává vnitřní energie konstantní), a to bude v důsledku do systému dodaného
nebo ze systému odebraného množství tepla, nebo v důsledku nějaké formy práce vykonané okolím na systém nebo systémem na okolí. Kladné U tedy udává úhrnnou energii, kterou soustava přechodem ze stavu A do stavu B z okolí zísChemická termodynamika
17
kala, ať již ve formě tepla nebo mechanické práce, nebo v jakékoliv jiné formě. Co daná soustava na energii získala,
ztratilo okolí. Přechod spojený s poklesem vnitřní energie (tj. když vnitřní energie stavu počátečního je větší než konečného. takže U je záporné) vede naopak k obohacení okolí energií na útraty systému.
Podstata první věty termodynamické, representované rovnicí (3.1), může být tedy shrnuta do
dvou bodů:
definuje nový pojem, vnitřní energii, pomocí dvou přímo měřitelných veličin, tepla a práce;
udává, že takto definovaná vnitřní energie je stavová veličina, tj. závisí pouze na stavu systému a
ne na jeho předchozí historii.
Přesto, že vnitřní energie, práce a teplo se vyjadřují ve stejných jednotkách, je mezi nimi určitý rozdíl. Zatímco
vnitřní energie U je stavová veličina, závisí množství tepla i množství vykonané práce na způsobu (cestě) převedení
soustavy z jednoho stavu do druhého, a nejsou tedy stavovými veličinami. Ke snazšímu pochopeni uvedeného rozdílu je
možno uvést analogii ze života: Do přehrady přitéká potok a právě prší: pokud se tak děje, je možno mluvit o „vodě
dešťové a potoční“. Jakmile však voda jednou v přehradě je, nemá smysl a také nemůžeme rozlišit, která (které molekuly vody) napršela a která ne. Víme jen, že je v přehradě třeba 10 miliónů m 3 vody. Podobné jsou pojmy teplo a práce
(obdoba „vody dešťové a potoční!) vázány na určitý děj, probíhající mezi systémy, kdežto vnitřní energie (voda v přehradě) je vlastností systému.
Pro snazší pochopení matematické formulace 1. termodynamické věty si ukážeme ještě analýzu vztahů práce, tepla
a vnitřní energie na dvou konkrétních příkladech:
Nejprve uvažujme spouštění břemene z vyšší polohy A do nižší B. Toho lze dosáhnout řadou způsobů. Tak jej lze
připevnit na jeden konec provazu, vedený přes vhodně umístěnou kladku, a druhý konec upevnit na zátěž, přibližně
stejné váhy, umístěnou v poloze B, kam chceme břemeno spustit. Břemeno počne klesat, a tím koná práci (zvedá zátěž)
a uvolňuje se jen malé množství tepla (třením provazu o kladku). Jiný způsob, jak dostat břemeno dolů, je nechat ho
klouzat po nakloněné rovině. Tím se získá méně práce, ale třením břemene o nakloněnou rovinu se uvolní větší množství tepla. Je možné volit různé dráhy pro posun břemene, které se budou lišit odporem proti jeho pohybu, takže vykonaná práce a uvolněné teplo budou pro různé cesty různé. Součet práce a tepla však bude ve všech případech stejný, pokud výchozí a konečný bod pohybu břemene budou pro všechny cesty stejné, a bude dán rozdílem vnitřní energie před a
po spuštění (v poloze A a B).
Jiným příkladem může být chemický systém: budeme sledovat např. vylučování mědi z roztoku její soli účinkem
méně ušlechtilého zinku.
(a) V otevřené nádobě (tj. za atmosférického tlaku) proběhne chemická reakce,
Zn (s) + CuSO4 (aq) = Cu (s) + ZnSO4 (aq)
při níž se do okolí uvolní určité množství tepla Qa, = –215,21 kJ/mol. Jelikož pracujeme v otevřené nádobě, nevykonal systém žádnou práci (objem se nezměnil), takže uvolněné teplo je zároveň celkovým množstvím energie, jež byla
předána do okolí, a představuje tedy pokles vnitřní energie systému,
Ua = Qa, = –215,21 kJ/mol
(b) Uvažovaná reakce však mohla proběhnout také jinou cestou, např. v galvanickém článku (viz Elektrochemie). Při
vhodném uspořádání produkuje článek elektrickou práci Wb = –213,83 kJ/mol a předá určité množství tepla do okolí.
Qb, = –1,38 kJ/mol. V tomto případě se s okolím vyměňuje celková energie
Ub = Qb + Wb = –1,38 – 213,83 = –215,21 kJ/mol
Změna vnitřní energie je tedy v obou případech stejná, tj. nezávislá na způsobu provedení reakce, čili je to stavová veličina, jak definuje první věta termodynamická. Naproti tomu tepelné zabarvení reakce a množství vykonané práce
jsou při různých způsobech provedení reakce různé.
Lze tedy říci, že
 Součet všech druhů energie v uzavřeném systému se nemění, ať uvnitř probíhají jakékoli pro-
cesy. Změna vnitřní energie izolovaného systému je nulová.
 Energii nelze z ničeho vyrobit, ani ji nelze zničit, je možné pouze převádět jednu formu energie v jinou. Zmizí-li někde určité množství energie, musí se objevit ekvivalentní množství
energie jinde.
 Z první věty plyne nemožnost konstrukce perpetua mobile prvního druhu: Není možno sestrojit stroj, který by trvale nebo periodicky dodával mechanickou energii, aniž by při tom nespotřeboval ekvivalentní množství jiné energie (pro cyklický děj je počáteční a konečný stav stejný a tedy U = 0)
 První věta termodynamická definuje pouze rozdíl vnitřních energií systému v konečném a počátečním stavu. Hodnota vnitřní energie systému muže být tak určena pouze vzhledem
k nějakému referenčnímu stavu (podobně jako udávání nadmořské výšky).
Chemická termodynamika
18
PRÁCE
Z fyziky víme, že v mechanice se práce vždy spojuje s působením síly. Je přitom lhostejné, nač síla působí – zda na hmotný bod, na soubor hmotných bodů, na spojité těleso nebo na soustavu těles. Jsou-li dány síly a vzdálenosti, o něž se posunula jejich působiště, můžeme vypočítat práci. Velikost práce, kterou vykoná síla, když se její působiště posune o vzdálenost dr ve směru jejího působení je dW = F dr. Svírá-li vektor síly a vektor dráhy úhel . platí dW = F cos . dr.
I když existuje více forem práce (objemová, elektrická, povrchová ...), budeme se v termodynamice setkávat většinou
s prací objemovou. Jako modelový systém si zvolíme tekutinu, např. plyn, uzavřenou ve válci s pístem, o němž se předpokládá, že se pohybuje bez tření. Mechanická práce pak vyplývá z objemových změn plynu, pokud jsou spojeny
s překováváním tlaku. Vnější tlak působící na píst o ploše A je pvn = F/A. Jestliže se píst účinkem vnější síly posune ve směru jejího působení (cos . = 1) o dr, je práce vykonaná touto silou (tj. vykonaná okolím na systém):
đWokolí = F cos . dr = pvn A dr = pvn dV
(3.2)
kde dV = A dr je změna objemu systému při posunutí pístu o dr. V termodynamice soustřeďujeme pozornost na samotnou soustavu a uvažujeme proto práci dodanou soustavě a práci odevzdané soustavou do okolí.
Pro uvažovanou soustavu tedy platí
đW = –pvn dV
(3.3)
Podle mezinárodní konvence označujeme práci dodanou soustavě, tj. soustavou přijatou jako kladnou a práci odevzdanou do okolí, tj. práci soustavou vykonanou jako zápornou. Je-li systém stlačován, jeho objem se zmenšuje, dV < 0 a đW je ve shodě s uvedenou konvencí kladné. Při expanzi se
objem systému zvětšuje, koná práci a đW < 0. Označíme-li symbolem p tlak uvnitř systému, pak při
kompresi platí p < pvn, při expanzi p > pvn. Symbol đ označuje neúplný diferenciál (práce je nestavová veličina, závisí na cestě- viz dále).
Vratný a nevratný děj
Rozdíl tlaku systému a vnějšího tlaku není důležitý pouze k posouzení zda dochází ke kompresi nebo expanzi, ale především k posouzení, zda uvažovaný děj probíhá vratně či nevratně. Při vratném (reverzibilním) ději se vnější a vnitřní tlak v každém okamžiku liší jen o infinitezimální hodnotu a směr děje lze libovolně malou změnou podmínek zastavit nebo obrátit jeho směr.
Při nevratném (ireverzibilním) ději se vnější a vnitřní tlak výrazně liší; infinitezimální změna vnějších podmínek nemá na průběh uvažovaného děje žádný vliv.
Např. při nevratné (skutečné) kompresi musí být vnější tlak větší než tlak systému, protože
píst musí překonávat tření mezi tělesem pístu a válcem, které bude tím větší, čím větší je rozdíl mezi oběma tlaky
(má-li systém pod pístem zůstat uzavřený),
doba komprese musí probíhat relativně krátkou dobu a proto je nutno použít větší sílu (tlak).
Klasická termodynamika ovšem dovede exaktně popisovat pouze rovnovážné stavy soustav a vratné
děje, jež v nich probíhají; její aplikace na nevratné děje je proto vždy spojena s určitými aproximacemi, jejichž oprávněnost je tím větší, čím více se průběh nevratného děje blíží průběhu děje vratného.
Pro uzavřené systémy, které nemohou vyměňovat s okolím jinou než objemovou práci, lze napsat
první větu termodynamickou ve tvaru:
dU = đQ – p dV
(3.4)
Výpočet objemové práce
Celkovou práci je třeba zjistit integrací vztahu (3.3):
V2
W=–
pvn dV
(3.5)
V1
k čemuž je nutno znát jakou funkcí objemu je tlak; tvar této funkce závisí na povaze děje. Ze vztahu
(3.4) a geometrického významu integrálu plyne, že číselně je objemová práce (popř. až na znaménko) rovna ploše pod křivkou pvn = f(V) (obr. 3-2). Velikost práce závisí nejen na počátečním (1) a
konečném (2) stavu, ale též na zvolené cestě. Porovnejme dvě cesty: první (obr. 3-2b), kdy nejprve
provedeme izobarickou expanzi do bodu A a pak izochorické snížení tlaku do bodu 2 a druhou (obr.
3-2c), při níž nejprve převedeme systém izochoricky do bodu B a následující izobarickou expanzí
do stavu 2. Jak plyne z různosti obsahu šedých ploch, je práce spojená s těmito ději různá. Porovnáme-li vratný a nevratný děj, je vždy nevratná práce větší než vratná.
Chemická termodynamika
19
pvn
(a)
1
pvn
(b)
A
1
2
V1
2
V1
V2
V
V2
V
pvn
(c)
1
2
B
V1
V
V2
Obr. 3-2 Geometrické znázornění práce v p-V diagramu
Při ději proti stálému vnějšímu tlaku pvn = konst. je objemová práce rovna:
W = –pvn (V2 – V1)
(3.6)
Jestliže systém expanduje proti nulovému vnějšímu tlaku (do vakua, pvn = 0), pochopitelně nekoná žádnou práci.
Při izochorickém ději (V = konst., dV = 0) je objemová práce vždy nulová.
Při vratném ději je možno vnější tlak nahradit vnitřním tlakem systému, pvn = p (rozdíl mezi
oběma tlaky lze pro výpočet práce u vratného děje zanedbat).
 Pro systém složený z n molů ideálního plynu, který přechází z objemu V1 na V2 a pro který
platí pvn = p = nRT/V platí:
V
p
W
n R T ln 2
n R T ln 1
(3.7)
V1
p2
kde p1 = nRT/V1 a p2 = nRT/V2.
 Pro systém složený z n molů reálného plynu, jehož stavové chování se řídí např. van der Waalsovou rovnicí
V2
n RT
V nb
(
W
V1
n2a
) dV
V2
n R T ln
V2 nb 2 1
n a(
V1 nb
V2
1
)
V1
(3.8)
při adiabatickém ději je đQ = 0 a z první věty termodynamické (rovnice (3.1)) plyne, že soustava
koná práci jen na útraty své vnitřní energie, đW = dU.
TEPLO
Jestliže propojíme dva systémy o různých teplotách tepelně vodivým spojením, proudí energie samovolně ze systému teplejšího do chladnějšího. Tato energie se nazývá teplo. Je závislá na rozdílu
teplot, na velikosti systému (látkovém množství n či hmotnosti m), na druhu látky, která tvoří systém i na podmínkách, za kterých se převod tepla děje ([p] , [V] apod.), tzn. stejně jako práce je teplo
procesní veličina.
Vymění-li systém s okolím určité množství tepla Q, změní se jeho teplota z T1 na T2 a platí, že
vyměněné teplo je úměrné rozdílu teplot:
Q C (T2 T1 ) C T
(3.9)
kde C je střední tepelná kapacita systému. Z experimentů vyplynulo, že tepelná kapacita je závislá
na teplotě. Přesná definice je proto dána limitou:
C
Q
T
lim
T
0
đQ
dT
(3.10)
a množství tepla, vyměněné s okolím integrálem
T2
Q
C dT
(3.11)
T1
Protože teplo je nestavová veličina (đ je neúplný diferenciál), je třeba k úplnému popisu předepsat
cestu:
Chemická termodynamika
20
za konstantního objemu (dV = 0) z první věty termodynamické pro teplo dostaneme
dQV = dU
(3.12)
Teplo vyměněné mezi systémem a okolím za konstantního objemu je rovno změně vnitřní energie systému.
Pro tepelnou kapacitu platí:
CV 1 U
Um
molární CVm
J mol–1 K–1
(3.13)
dQV
U
n
n T V
T V
CV
dT
T V
CV 1 U
specifická CVsp
J kg–1 K–1
(3.14)
m m T V
za konstantního tlaku platí:
dQp = dU + p dV = d(U + p V)
(3.15)
Výraz U + p V , s nímž se ve fyzikálně-chemické praxi často setkáváme, definuje novou stavovou funkci, entalpii
H = U + pV
(3.16)
Teplo vyměněné mezi systémem a okolím za konstantního tlaku je rovno změně entalpie systému.
Pro tepelnou kapacitu platí:
Cp
dQ p
dT
H
T
molární
p
C pm
specifická C p sp
Cp
n
1
n
Cp
m
H
T
1
m
Hm
T
p
H
T
J mol–1 K–1
(3.17)
p
J kg–1 K–1
(3.18)
p
Teplotní závislost tepelných kapacit
Zatímco střední tepelnou kapacitu C považujeme v daném teplotním intervalu za konstantní, je
pravá tepelná kapacita C závislá na teplotě. Tato závislost je vyjadřována empirickými mocninovými rovnicemi, např.:
C = a + bT + cT2 + dT–1 + eT–2 + ...
(3.19)
kde a, b, c, d, e... jsou konstanty (některé nemusí být uvažovány), jejichž hodnoty jsou určovány
z experimentálních dat (ta jsou měřena kalorimetricky). Hodnoty konstant jsou uváděny
v tabulkách. Tvar teplotní závislosti je stejný pro CVm i pro Cpm.
Tepelné kapacity látek ve stavu ideálního plynu
Z kinetické teorie ideálního plynu (nebude probírána v rámci tohoto předmětu) lze odvodit, že
pro ideální jednoatomový plyn platí:
CVm = 3/2 R a Cpm = 5/2 R
(3.20)
5
7
pro ideální dvouatomový plyn za nepříliš vysokých teplot: CVm = /2 R a Cpm = /2 R
(3.21)
Tepelné kapacity pevných látek
Pro odhad tepelné kapacity prvků lze použít Dulongova-Petitova pravidla: součin specifické tepelné
kapacity a atomové hmotnosti prvku má přibližně stálou hodnotu, 26,4 J K–1 mol–1. Molární tepelnou kapacitu sloučenin lze odhadnout podle Neumannova-Koppova pravidla: molární teplo sloučeniny je rovno součtu atomárních tepel prvků, které sloučeninu tvoří.
Rozdíl mezi tepelnými kapacitami Cp a CV
Rozdíl mezi tepelnými kapacitami za konstantního tlaku a objemu lze vyjádřit pomocí stavového
chování uvažovaného systému (nebudeme si jej odvozovat ani pamatovat, stačí vědět, že existuje):
C p CV
H
T
p
U
T
T
V
V
T
2
p
p
V
TV
2
(3.22)
T
Parciální derivace vyjádříme buď z příslušné stavové rovnice, nebo jak ukazuje poslední člen ve
vztahu (3.22), pomocí koeficientu roztažnosti a stlačitelnosti.
Pro ideální plyn použijeme stavovou rovnici ideálního plynu a dostaneme tzv. Mayerův vztah:
Cp – CV = n R
(3.23)
Pro pevné látky a kapaliny je možno rozdíl (Cp – CV ) vypočítat pomocí koeficientů roztažnosti a
stlačitelnosti (vztah (3.22)), ale lze říci, že obecně je velmi malý.
Chemická termodynamika
21
Tepelná kapacita směsí
Pro systém tvořený směsí ideálních plynů platí vztahy:
C pm
xi C pm,i , CVm
i
xi CVm,i
(3.24)
i
kterých je často užíváno i k odhadu reálných směsí plynných, kapalných i pevných.
Vnitřní energie a entalpie ideálního plynu
je pouze funkcí teploty, nezávisí na tlaku ani na objemu (na rozdíl od reálného plynu)
dU = dQV = CV dT
,
dH = dQp = Cp dT
U = CV (T2 – T1) ,
H = Cp (T2 – T1)
(3.25)
(3.26)
Termochemie
se zabývá stanovením tepla vyměněného s okolím při průběhu chemické reakce. Toto teplo se
označuje jako reakční teplo.
Zápis chemické reakce
Chemickou reakci je možno zapsat klasickým způsobem:
aA+bB+ =rR+sS+
(3.27)
kde malá písmena symbolizují stechiometrické koeficienty, velká písmena reagující látky. Pro některá odvození je výhodné použít zápisu ve tvaru:
(tj. r R + s S – a A – b B = 0)
(3.28)
i Li 0
i
kde symbolem Li je označena i-tá látka reakční směsi a νi její stechiometrický koeficient. Byla zavedena konvence, že pro výchozí látky jsou stechiometrické koeficienty záporné, pro produkty
kladné (tj. νA = −a, νB = −b, νR = +r, νS = +s,).
Skupenské stavy látek označujeme pomocí symbolů v závorkách za jejich chemickými vzorci.
Symbol (g) značí plyn. (ℓ) kapalinu a (s) tuhou látku. U plynných látek bývá uváděn i tlak, u tuhých
látek je-li to nutné, modifikace, např. C(s, grafit). Je-li látka v roztoku, uvádí se koncentrace tohoto
roztoku, např. (aq, 0,1 M) značí, že jde o vodný roztok o koncentraci 0,1 mol dm–3 (jde-li o jiné
rozpouštědlo, uvedeme v závorce, není-li to zřejmé z textu).
Aby pojem reakční teplo byl jednoznačný, je třeba
uvést za jakých podmínek reakce probíhá. Za konstantního objemu je reakční teplo rovno reakční vnitřní energii ΔrU. Protože však převážná většina reakcí probíhá za konstantního tlaku, budeme pod reakčním teplem, pokud nebude uvedeno jinak, rozumět reakční entalpii ΔrH; vztah
mezi oběma druhy reakčních tepel udává definiční rovnice entalpie (3.16): reakční teplo za stálého tlaku se rovná reakčnímu teplu za stálého objemu zvětšenému o objemovou práci vykonanou soustavou:
ΔrH = ΔrU + p ΔV
(3.29)
Pro reakce v kondenzovaných soustavách (tj. mezi tuhými a kapalnými látkami) jsou objemové
změny při reakci zanedbatelné, takže ΔrH ≈ ΔrU ; zúčastní-li se reakce také plyny, je možno za
nízkých tlaků použít stavové rovnice ideálního plynu: p ΔV = Δng RT, kde Δng je rozdíl součtu
počtu molů plynných reakčních zplodin a součtu počtu molů plynných výchozích látek;
pamatovat na to, že údaj o reakčním teple se týká izotermního a stechiometrického průběhu reakce, tzn. že na počátku reakce jsou přítomny pouze látky výchozí a na konci látky konečné. Jednotkou reakčního teplo je J/mol nebo kJ/mol přičemž mol znamená mol „reakčního obratu“, tj.
např. zreaguje-li reakcí (3.27) a mol látky A s b mol látky B za vzniku r mol látky R a s mol látky S. Jestliže vynásobíme levou i pravou stranu rovnice (3.27) dvěma, je i reakční teplo dvojnásobné (proběhly dva reakční obraty). V případě, že by reakce probíhala obráceně, byla by hodnota reakčního tepla stejná, ale opačného znaménka. Reakce, jejichž ΔrH > 0 potřebují ke svému
průběhu dodávat teplo z okolí; jsou označovány jako endotermní. Při reakcích exotermních se
teplo uvolňuje; ΔrH < 0.
předpokládat, že v uvažované soustavě probíhá pouze jediná reakce
Chemická termodynamika
22
Hessův zákon
V současné době existuje přímo ohromující množství údajů o reakčních teplech reakcí všech možných typů, naměřených za nejrůznějších experimentálních podmínek. Na druhé straně je zřejmé, že počet reakcí, o kterých existují
termodynamické údaje, je pouhým zlomkem reakcí, které jsou nám dnes známy; snažit se o změření reakčních tepel všech myslitelných reakcí by tedy byl
nereálný úkol.
Naštěstí to není nutné. Protože reakční teplo za konstantního tlaku je rovno
změně entalpie soustavy při dané reakci a o entalpii víme, že je to stavová
funkce, závisí její změna pouze na stavu soustavy před reakcí a po ní, nikoliv
na cestě, jakou se soustava při reakci ubírala. K tomuto závěru dospěl na základě experimentálních dat již r.1840 G.H. Hess:
Reakční teplo dané reakce nezávisí na tom, zda reakce proběhla přímo, nebo ve více po sobě následujících krocích.
Z Hessova zákona vyplývá, že reakční teplo určité reakce lze vypočítat z reakčních tepel takových
reakcí, které vhodnou algebraickou kombinací dají reakci hledanou, což není omezeno jen na chemické reakce, ale i na změny fyzikální. Pro praktické účely, zejména pro účely tabelace termochemických dat, je třeba zúžit výběr typů reakcí, jejichž reakční tepla je vhodné v literatuře uvádět;
nejčastěji jsou tabelována standardní slučovací a spalná tepla.
Standardní slučovací teplo slH(T) chemické sloučeniny je rovno změně entalpie doprovázející
vznik jednoho molu dané sloučeniny z prvků při teplotě T, kde jak výchozí prvky, tak vznikající
sloučenina jsou ve svých standardních stavech.
Byla zvolena konvence, podle níž
je entalpie prvků v jejich standardních stavech při libovolné zvolené teplotě rovna nule.
Při výpočtu reakčního tepla ze slučovacích tepel je možno reakci myšlenkově rozdělit na dvě etapy:
v prvé se výchozí látky rozštěpí až na molekuly prvků a v druhé se tyto prvky sloučí na reakční
produkty. Pro celkovou změnu entalpie pak platí:
(3.30)
rH
i sl H i
i
tedy např. pro reakci (3.26):
r
rH
sl H R
s
sl HS
a
sl H A
b
sl H B
(3.31)
Standardní spalné teplo spH (T) chemické sloučeniny je rovno změně entalpie doprovázející
spálení jednoho molu dané sloučeniny se stechiometrickým množstvím kyslíku při teplotě T, kdy
jak výchozí prvky, tak produkty spalování, jsou ve svých standardních stavech. K úplné charakterizaci je zde nutno udat rovněž reakční produkty a jejich stav (např. zda při spalování vzniká voda
v kapalném či plynném stavu)

Při výpočtu reakčního tepla ze spalných tepel je opět možno reakci myšlenkově rozdělit na dvě etapy: v prvé se výchozí látky spálí až na CO2 a H2O (popř. další produkty spalování), z nichž v druhé
etapě vzniknou reakční produkty. Pro celkovou změnu entalpie pak platí:
(3.32)
rH
i sp H i
i
tedy např. pro reakci (3.26):
a
rH
sp H A
b
sp H B
r
sp H R
s
sp H S
(3.33)
Pozn: Na rozdíl od slučovacích tepel mívají spalná tepla značné (záporné – spalování je exotermní děj) hodnoty. Protože při výpočtu reakčních tepel odečítáme spalná tepla produktů od spalných tepel výchozích látek, tj. velká čísla od velkých čísel, je výsledná hodnota zatížena procentuálně větší chybou, než jakou mají spalná tepla látek, které se reakce
zúčastní.
Chemická termodynamika
23
Závislost reakčních tepel na teplotě – izotermní průběh reakce
Reakční teplo, které vypočteme z tabelovaných termodynamických dat (např. slučovacích tepel),
platí pro tu teplotu, pro kterou jsou známa příslušná výchozí data (nejčastěji pro 298,15 K). V praxi
nás však daleko častěji zajímá hodnota reakčního tepla při jiné, obvykle vyšší teplotě.
Uvažujme jako příklad systém, v němž probíhá chemická reakce (3.27) a předpokládejme, že jsme
v tabulkách nalezli termodynamická data pro teplotu To a vypočítali jsme podle Hessova zákona

rH (To). Potřebujeme zjistit reakční teplo této reakce při T, tj. teplo vyměněné s okolím při konstantním tlaku při reakci (3.27), jestliže výchozí látky i produkty mají teplotu T. Protože nemáme termodynamická data při teplotě T pro přímý výpočet rH(T), tj. po cestě vyznačené na obr. 3-3 čárkovanou čarou, využijeme skutečnosti, že entalpie je stavová funkce a zvolíme náhradní cestu:
výchozí látky (a molů látky A a b molů látky B) převedeme z teploty T na To; přitom systém
vymění s okolím teplo Q1.
Q1 = a CpmA (To – T) + b CpmB (To – T)
(3.34)
necháme proběhnout reakci při To; teplo vyměněné s okolím je rH(To) (to umíme vypočítat) a
dostaneme produkty při teplotě To
Q2 = rH(To)
(3.35)
produkty (r molů látky R a s molů látky S, předpokládáme, že reakce proběhne kvantitativně)
převedeme z teploty To na teplotu T; teplo vyměněné s okolím je Q3.
Q3 = r CpmR (T – To) + s CpmS (T – To)
(3.36)
při T
rR + sS
při T
aA + bB
T
rH
T
(T )
Q1
Obr. 3-3 Schéma výpočtu teplotní závislosti reakčního tepla
Q3
Q2
rH
(To )
To
To
aA+bB
při To
rR+sS
při To
Součet entalpických změn při těchto třech dějích Q1 + Q2 + Q3 je roven reakčnímu teplu při T:

rH (T) = a CpmA (To – T) + b CpmB (To – T) +
+ rH(To) + r CpmR (T – To) + s CpmS (T – To)
(3.37)
Rovnice (3.37), označovaná jako Kirchhoffova věta, umožňuje vypočet reakčního tepla při libovolné teplotě T ze známého reakčního tepla při jedné teplotě To a ze známé teplotní závislosti molárních tepelných kapacit všech látek, které se reakce zúčastní.
Obecná entalpická bilance – neizotermní průběh reakce
V praxi se často setkáváme se situací, kdy sice daný děj probíhá za konstantního tlaku, ale výchozí
látky i produkty mají různé teploty podle schématu na obr. 3-4. Množství tepla, které se v průběhu
reakce vymění s okolím, vypočítáme opět stejným způsobem, jakým jsme odvodili Kirchhoffovu
rovnici: celý děj myšlenkově rozdělíme na tři etapy:
Výchozí látky tentokrát nejsou ve stechiometrickém poměru, a jsou přítomny i látky, které se reakce neúčastní (inerty). Jednotlivé složky jsou přiváděny do reaktoru při různých teplotách:
nA0 molů látky A přichází při teplotě TA0,
nB0 molů látky B přichází při teplotě TB0,
a
nI molů inertu I přichází při teplotě TI0
Každou z výchozích látek převedeme na teplotu Tref, při níž známe termodynamická data (např.
slučovací nebo spalné entalpie) a při této teplotě tedy můžeme vypočítat reakční entalpii

rH (Tref).
Chemická termodynamika
24
a produkty reakce převedeme z Tref na teploty, s kterými odcházejí z reaktoru:
nR molů produktu R při teplotě TR,
nS molů produktu S při teplotě TS,
nI molů inertu I při teplotě TI
a nezreagované
nA molů látky A při teplotě TA,
nB molů látky B při teplotě TB,
nR R
TA0
TI0
TB0
nA0 A
TR
nA A
TA
TI
nI I
nI I
nS S
Q5
Q3
nB0 B
nB B
Q6
TB
Q7
Q2
Q8
Q1
Q4
Tref
TS
rH
Q9
(Tref )
Obr. 3-4 Schéma entalpické bilance při neizotermním průběhu reakce
Látková množství odcházejících látek vyjádříme pomocí jedné veličiny, rozsahu reakce. Ten si můžeme představit jako počet „reakčních obratů“, tj. jako číslo, které udává kolikrát proběhla daná reakce tak jak je zapsána stechiometrickou rovnicí. Vzhledem k definici je zřejmé, že jeho hodnota
nezáleží na tom, pomocí které reakční složky je definován:
ni ni 0
i
B = –b , R = +r , S = +s ) by tedy platilo
nA nA0 nB nB0 nR nR0 nS nS0
a
b
r
s
Jestliže nR0 = 0 a nS0 = 0, dostaneme
nA = nA0 – a ,
nB = nB0 – b
,
nR = r
,
Pro reakci (3.27) (
A
= –a ,
nS = s
Celkové teplo vyměněné s okolím je dáno součtem všech dílčích tepelných změn:
Q = Q1 + Q2 + Q3 + Q4 + Q5 + Q6 + Q7 + Q8 + Q9 =
= nA0 CpmA (Tref – TA0) + nB0 CpmB (Tref – TB0) + nI CpmI (TI0 – Tref) +
+ nR CpmR (TR – Tref) + nS CpmS (TS – Tref) + nI CpmI (TI0 – Tref) +
+ nA CpmA (TA – Tref) + nB CpmB (TB – Tref)

rH
(Tref) +
(3.38)
Adiabatická reakční teplota
Jestliže proběhne chemická reakce v uzavřené soustavě adiabaticky, dosáhnou reakční produkty
(včetně případně přítomných inertů) určité konečné teploty, jež se označuje jako adiabatická reakční teplota; pokud se jedná o hoření, používá se název teoretická teplota plamene. Protože systém
nevyměňuje s okolím teplo, platí:
Q=0
(3.39)
Ve spojení s rovnicí (3.38) je možno zjistit neznámou teplotu Tad :

ni,vých C pm,i (Tref Ti,vých ) +
ni,kon C pm,i (Tad Tref ) = 0 (3.40)
rH (Tref) +
i
i
Skutečná teplota plamene je vždy menší než takto vypočtená teoretická teplota plamene, neboť jednak při praktickém provedení vždy dochází k určitým tepelným ztrátám a dále nemusí vždy dojít
k úplnému dokončení reakce.
Chemická termodynamika
25
DRUHÁ VĚTA TERMODYNAMICKÁ
Samovolné děje
Podle první věty termodynamické nelze posoudit, jakým směrem bude děj, který je termodynamicky principiálně možný, probíhat. Zkušenost přitom ukazuje, že v přírodě probíhají samovolné procesy vždy jen v jednom směru, např. teplo přechází z tělesa teplejšího na těleso chladnější, difuze
látek probíhá ve směru od vyšší koncentrace k nižší, plyn proudí z míst vyššího tlaku na nižší a nikdy tomu není naopak.
Děje, které probíhají v soustavách samovolně, jsou děje nevratné. Kritérium spontánnosti nijak
nevyplývá z první věty, protože spontánně probíhající děje jsou někdy spojeny se vzrůstem vnitřní
energie, jindy s jejím úbytkem. Z první věty vyplývá pouze to, že při změnách v izolované soustavě
zůstává celková energie konstantní.
Samovolnost procesů je možno demonstrovat na odrazu míčku od tuhé podložky (obr. 3-7) – po každém odrazu
míček skočí níž, až nakonec zůstane na podložce. Snižování výšky odrazu je způsobeno třením mezi povrchem míčku a
podložkou, které se mění na teplo, tj. na neuspořádaný pohyb molekul. Podložka se nepatrně zahřeje a odraz se zmenšuje. Obrácení děje by vyžadovalo, aby se část energie podložky soustředila do jediného předmětu (míčku), tj. aby se pohyb molekul uspořádal směrem vzhůru v okamžiku odrazu míčku od podložky. Podle všech dosavadních zkušeností je
to nemožné.
samovolný
proces
Obr. 3-7 Mechanický model samovolného děje
Samovolné tlumení odrazů míčku při dopadech na pevný podklad
I1
I2
I2
I1 , I2 , I3 impulzy předávané podložce
I 1 , I 2 , I 3 impulzy předávané podložce
I3
I3
Zvyšování neuspořádanosti ukazuje tedy směr samovolného
děje. Obrácený proces je nepravděpodobný, prakticky nemožný.
I1
Entropie
Pro kvantitativní vyjádření této myšlenky zavádí druhá věta termodynamická novou termodynamickou funkci – entropii. Termodynamický výklad entropie je založen na skutečnosti, že rozdělení
energie soustavy souvisí s množstvím tepla, které se při procesu vyměnilo. Podle první věty termodynamické jsou teplo a práce (mechanická, elektrická nebo jakákoli jiná) zcela ekvivalentní. To
znamená, že určité množství tepla odpovídá zcela určitému množství práce a naopak. Neznamená to
ale, že jsou ekvivalentní i možnosti úplné přeměny jedné z těchto forem energie v druhou. Ze zkušenosti je známo, že práci jakéhokoliv druhu lze poměrně snadno přeměnit na teplo prakticky bez
omezení. Lopatkové míchadlo, které se otáčí v kapalině, nebo odporový drát ponořený do kapaliny,
kterým prochází elektrický proud, jsou zařízeními, která mění soustavně práci mechanickou, resp.
elektrickou na teplo. Slovem soustavně chceme říci to, že práci lze tímto způsobem měnit v teplo
prakticky neomezeně. Systém, který přeměnu zprostředkuje, je na začátku i na konci děje ve stejném stavu. Opačný děj, přeměna tepla v práci, je mnohem obtížnější a se stal předmětem trvalého
zájmu inženýrské praxe od chvíle, kdy James Watt roku 1769 sestrojil parní stroj. Míchadlo vnořené do nádoby s teplou vodou se samo neroztočí ani zahřátí odporového drátu nezpůsobí vznik elektrického proudu. Přitom je soustavná přeměna tepla na práci z praktického hlediska velmi důležitá.
Jednorázová přeměna tepla v práci ovšem omezena není.
Chemická termodynamika
26
Clausius (1854) definoval entropii rovnicí, která představuje matematickou formulaci druhé věty termodynamické:
dQrev
dS
(3.41)
T
Entropie je stavová funkce, závisí jen na stavu systému, ne na cestě po níž systém do uvažovaného stavu přišel (na rozdíl od tepla). Proběhne-li v systému nějaký děj je příslušná změna entropie
určena stavem systému na začátku (A) a na konci děje (B):
S = SB – SA
(3.42)
dQ
Pro nevratné děje platí:
(3.43)
dS
T
Druhou větu termodynamickou lze slovně vyjádřit:
Existuje stavová funkce entropie S, jejíž totální diferenciál je větší nebo roven výrazu dQ/T , kde
Q je teplo, které systém vyměňuje s okolím a T absolutní teplota. Znaménko > platí pro nevratné ,
znaménko = pro vratné děje
Je tedy možno psát:
dS
dQ
T
ir
rev
(3.44)
Pro soustavu adiabatickou a pro soustavu izolovanou, které nevyměňují s okolím teplo (dQ = 0) má
rovnice (3.44) tvar:
dS 0 [ad, izol]
(3.45)
V adiabatických a v izolovaných soustavách entropie při všech nevratných dějích roste;
v rovnováze, tj. ve stavu, kdy mohou probíhat jen vratné děje, se nemění.
Entropie je
mírou nevratnosti děje
mírou pravděpodobnosti
mírou neuspořádanosti systému
mírou informace
Samovolný přechod ze stavu méně pravděpodobného do stavu pravděpodobnějšího je provázen vzrůstem
neuspořádanosti soustavy a proto entropie, která vzrůstá při spontánních dějích může být považována také za
míru uspořádanosti či neuspořádanosti soustavy. Ideálnímu krystalickému stavu, který se vyznačuje vysokým stupněm uspořádání, příslušejí nejmenší hodnoty entropie, a to tím nižší, čím nižší je teplota. Zvyšováním teploty se vlivem tepelného pohybu narušuje dokonalá uspořádanost ideálního krystalu za stálého růstu
entropie. Při dosažení bodu tání se ruší krystalová mřížka a tento přechod k nižšímu stupni uspořádání je
provázen náhlým vzrůstem entropie. Další vzrůst entropie nastává při přechodu ze skupenství kapalného do
skupenství plynného, ve kterém již chybí jakákoli uspořádanost, neboť molekuly plynu se pohybují zcela
chaoticky. Tato neuspořádanost ještě dále roste s klesajícím tlakem a rostoucí teplotou, takže plyn za extrémně nízkých tlaků a vysokých teplot představuje stav dokonale neuspořádaný. Souvislost mezi vzrůstem
entropie a přechodem k větší neuspořádanosti je zcela obecná a lze ji nalézt jak u dějů fyzikálních tak i chemických.
Změna entropie při izotermních vratných dějích
je dána integrálem definiční rovnice (3.44):
Qrev
(3.46)
S
T
Příkladem izotermních vratných dějů, které navíc probíhají za stálého tlaku jsou vratné fázové přechody (vypařování, tání, modifikační přeměny), pro které platí Qrev = fázH (index fáz označuje příslušnou fázovou přeměnu):
fáz H
[T, p, rev]
(3.47)
fáz S
T
Chemická termodynamika
27
Závislost entropie na teplotě a objemu (pro ideální plyn)
Pro ideální plyn, jehož vnitřní energie je pouze funkcí teploty, a konstantní tepelnou kapacitu platí
S ( S2 S1 )
změna
n CVm ln
T2
T1
s teplotou
za konst.V
n R ln
V2
V1
s objemem
za konst.T
Závislost entropie na teplotě a tlaku (pro ideální plyn)
T
p
S ( S2 S1 ) nC pm ln 2 n R ln 2
T1
p1
změna
s teplotou
za konst.p
(3.48)
(3.49)
s tlakem
za konst.T
Obecně jsou Cp i CV funkcemi teploty, danými empirickými mocninovými vztahy. Závislost entropie na tlaku , popř. na objemu při konstantní teplotě je pro systémy, které se nechovají ideálně, třeba
vyjádřit z příslušné stavové rovnice, která popisuje chování uvažovaného systému
Spojené formulace I. a II. věty termodynamické
Pro uzavřený homogenní systém, který koná jen objemovou práci a všechny v něm probíhající děje
jsou vratné, má první věta termodynamická tvar:
dU = dQrev – p dV
(3.50)
Jestliže dosadíme z druhé věty termodynamické dQrev = T dS, dostaneme relaci, nazývanou spojená
formulace první a druhé věty termodynamické:
dU = T dS – p dV
(3.51)
Proti dříve uvedeným formulacím I. a II. věty TD má rovnice (3.51) tu výhodu, že se v ní vyskytují pouze stavové veličiny systému a lze ji proto použít pro výpočet libovolné změny U, S,
V při ději, při němž známe počáteční a konečný stav systému.
Spojením rovnice (3.51) s diferenciálním tvarem definice entalpie (dH = dU + p dV + V dp), dostaneme jiný tvar spojené formulace:
dH = T dS + V dp
(3.52)
GIBBSOVA ENERGIE A HELMHOLTZOVA ENERGIE
PODMÍNKY ROVNOVÁHY A SAMOVOLNOSTI DĚJE
V souvislosti s druhou větou termodynamickou bylo ukázáno, jakým způsobem je možno použít
změny entropie k předpovědi, zda je daný děj vůbec možný. Pro izotermní děj bylo dostatečným
kritériem splnění podmínky dS > dQ/T.
Chemické reakce, popř. fyzikální změny však probíhají nejčastěji nejen při konstantní teplotě, ale i při konstantním tlaku, popř. konstantním objemu. Pro tyto případy je užitečné zavést do
termodynamiky další funkce.
Soustava izotermicko-izobarická; Gibbsova energie
Za konstantní teploty a tlaku má podmínka (3.44) tvar
dH ir
, popř. T dS dH [T, p]
(3.53)
dS
T rev
(znaménko rovnosti platí pro vratný děj, nerovnost pro nevratný, samovolný děj). Po úpravě
dH – T dS 0
(3.54)
Chemická termodynamika
28
Protože teplota je konstantní, platí T dS = d(TS) a dH – d(TS) = d(H – TS). Tato kombinace stavových funkcí představuje novou termodynamickou funkci, Gibbsovu energii:
G=H–TS
(3.55)
dG = dH – T dS – S dT = T dS + V dp – T dS – S dT = – S dT + V dp [T, p]
(3.56)
Rovnice
dG 0
[T, p]
(3.57)
tedy představuje kritérium pro posouzení, zda proces vedený izotermicky-izobaricky je uskutečnitelný.
Spěje-li systém za konstantní teploty a tlaku do rovnováhy, Gibbsova energie klesá, za rovnováhy
je minimální. V rovnováze se Gibbsova energie nemění.
Soustava izotermicko-izochorická; Helmholtzova energie
Za konstantní teploty a objemu má podmínka (3.44) tvar:
dU ir
, popř. T dS dU [T, V]
T rev
Stejným postupem jako v předcházejícím odstavci dostaneme:
dS
dU – T dS
0
(3.58)
(3.59)
Kombinace stavových funkcí U, T a S představuje další novou termodynamickou funkci, Helmholtzovu energii:
F=U–TS
dF = dU – T dS = T dS – S dT – p dV – T dS = – S dT – p dV [T, V]
(3.60)
Rovnice
dF
0
[T, V]
(3.61)
představuje kritérium pro posouzení, zda proces vedený izotermicky-izochoricky je uskutečnitelný.
Spěje-li systém za konstantní teploty a objemu do rovnováhy, Helmholtzova energie klesá, za
rovnováhy je minimální. V rovnováze se Helmholtzova energie nemění.
SYSTÉMY KTERÉ MOHOU KONAT NEOBJEMOVOU PRÁCI
Dosud jsme uvažovali systémy, které mohou konat pouze objemovou práci. Pro další úvahy rozdělíme práci, kterou systém vyměňuje s okolím na objemovou, danou součinem –p dV a neobjemovou, đW někdy označovanou také jako práce užitečná (např. elektrická, povrchová, magnetická
apod.). Pro vnitřní energii pak platí:
dU = đQrev + đWrev = T dS – p dV + đW rev
(3.62)
dU + p dV – T dS = đW rev
(3.63)
Za konstantního tlaku a teploty je dU + p dV = dH a tedy
dG = dW rev , resp. G = W rev
(3.64)
Užitečná práce soustavě dodaná se projeví zvýšením Gibbsovy energie; reverzibilně vykonaná neobjemová práce je rovna úbytku Gibbsovy energie.
Za konstantního objemu a teploty (dV = 0) dostaneme
dU – T dS = dF = dW rev
(3.65)
Užitečná práce dodaná soustavě při ději za konstantního objemu a teploty se projeví zvýšením Helmholtzovy energie; reverzibilně vykonaná neobjemová práce je rovna úbytku Helmholtzovy energie.
Chemická termodynamika
29
Chemický potenciál
Helmholtzova a Gibbsova funkce mají hlavní význam jako kritéria termodynamické rovnováhy.
Nejčastěji používaná podmínka rovnováhy pro uzavřenou soustavu, která nevyměňuje s okolím neobjemovou práci, je za konstantní teploty a tlaku vyjádřena nulovou změnou Gibbsovy energie,
dG = 0. Tato rovnice je ovšem zcela obecná a týká se celého systému. Pro konkrétní případy je nutno ji přeformulovat tak, aby obsahovala veličiny týkající se jednotlivých složek. K tomuto účelu definoval J.W. Gibbs chemický potenciál.
Pro Gibbsovu energii soustavy o k složkách, jejichž látková množství jsou n1, n2, … nk, platí:
G = G(T, p, n1, n2, … , nk)
(3.66)
Totální diferenciál je pak dán vztahem:
dG
G
dT
T p, n
j
G
dp
p T,n
j
G
n2
G
dn1
n1 T , p, n
j 1
dn2
T , p, n j 2
G
n3
G
nk
dn3
T , p, n j 3
dnk
(3.67)
T , p, n j k
Parciální derivace ( G/ T)p,nj má význam změny Gibbsovy energie způsobené jednotkovou změnou
teploty za konstantního tlaku a složení (látkových množství jednotlivých složek); první člen tedy
představuje příspěvek k celkové změně Gibbsovy energie konstantního tlaku a složení. Z porovnání
se vztahem (3.56) pro tuto derivaci plyne
G
T
= –S
(3.68)
p, n j
Druhý člen je změna Gibbsovy energie, způsobená jednotkovou změnou tlaku za konstantní teploty
a složení.
G
=V
(3.69)
p T,n
j
Parciální derivace ( G/ n1)T, p, nj 1 je změna Gibbsovy energie způsobená jednotkovou změnou
látkového množství složky 1, jestliže teplota a tlak jsou konstantní a nemění se ani látková množství
všech ostatních složek až na složku 1. Podobný je i význam dalších parciálních derivací. Tyto veličiny jsou označovány jako chemické potenciály:
G
(3.70)
i
ni T , p, n
j i
Pro jednosložkové systémy je chemický potenciál roven molární Gibbsově energii,
G
n
= Gm
(3.71)
T, p
Chemický potenciál usnadňuje rozbor otevřených i uzavřených soustav, v nichž se mění složení.
Má v termodynamice důležitou funkci, analogickou významu teploty a tlaku. Podobně jako je teplotní rozdíl příčinou, že teplo přechází z jednoho tělesa na druhé, tlakový rozdíl určuje pohyb plynu
z jednoho prostoru do druhého, je možno pokládat rozdíl chemických potenciálů za příčinu chemické
reakce nebo snahy složky difundovat z jednoho místa soustavy do jiného. Stejně jako tlak a teplota, je
i chemický potenciál intenzivní vlastností soustavy. Rovnici (3.67) je pak možno psát ve tvaru:
dG
S dT V dp
i dni
(3.72)
i
Chemická termodynamika
30
Za konstantní teploty a tlaku je
dG
i dni
(3.73)
i
Součin i dni tedy udává zvětšení neobjemové práce, kterou je soustava schopna konat při zvýšení látkového množství i-té složky o dni. Kritérium rovnováhy pro uzavřenou soustavu, která nevyměňuje
s okolím neobjemovou práci, vyjádřené pomocí chemických potenciálů, má pak tvar:
(3.74)
i dni = 0
i
Chemický potenciál ideálního plynu
Za konstantní teploty pro molární Gibbsovu energii ideálního plynu a tedy pro jeho chemický potenciál ze spojené formulace první a druhé věty (rovnice (3.56)) po dosazení ze stavové rovnice ideálního plynu dostaneme
RT
dGm = d = Vm dp =
dp = RT d ln p
(3.75)
p
Integrací od standardního stavu:
p
– st = RT ln st
(3.76)
p
Pro chemický potenciál složky v ideální směsi obdobně platí
p
st
RT ln sti
(3.77)
i
i
p
kde pi = xi p je parciální tlak složky i. V případě směsi, která by se neřídila stavovou rovnicí ideálního plynu by tento výraz byl mnohem složitější.
Aktivita
Pro usnadnění popisu reálných směsí byla definicí
i
st
i
RT ln ai
(3.78)
zavedena pomocná funkce – aktivita, která představuje bezrozměrnou míru rozdílu chemických potenciálů v uvažovaném a standardním stavu. Numerická hodnota aktivity závisí tudíž mimo jiné i na
volbě standardního stavu. Je nutné uvážit, který standardní stav je pro řešení daného problému nejvhodnější. I když standardní stav látky lze volit v podstatě libovolným způsobem, přidržujeme se
z praktických důvodů ustálené volby:
Plyn v ideálním stavu za tlaku pst = 101,325 kPa při teplotě soustavy. Pro aktivitu složky i ve
směsi za předpokladu ideálního chování platí:
ai
pi
p
st
xi p
p st
Pro reálné systémy je zaváděna korekce – fugacitní koeficient ,
pi
xi p
ai
i
i
p st
pst
(3.79)
(3.80)
Fugacitní koeficient může být vypočten z experimentálních dat o stavovém chování. Nejjednodušší
výpočet je založen na teorému korespondujících stavů.
Čistá složka za teploty a tlaku systému. Tento standardní stav se používá u kondenzovaných (tj. kapalných nebo pevných) látek, které za dané teploty a tlaku mohou existovat jako čisté kondenzované
látky. Pro ideální směs, je aktivita je rovna molárnímu zlomku:
ai = xi ,
(3.81)
Chemická termodynamika
31
Pro reálné směsi je odchylka od ideálního chování vyjadřována pomocí aktivitního koeficientu
ai = i xi ,
(3.82)
neboť molární zlomek složky ve standardním stavu je roven jedné (jde o čistou látku). Aktivitní
koeficient i je obecně funkcí teploty a složení směsi (vliv tlaku se u kondenzovaných fází zanedbává); pro čistou látku má hodnotu i = 1. Je-li kondenzovaná fáze tvořena pouze jednou látkou,
je aktivita této látky rovna jedné.
Standardní stav jednotkové koncentrace (nekonečného zředění) se používá pro látky v roztoku
(pro rozpouštědlo volíme standardní stav čisté kondenzované látky), které za dané teploty a tlaku
buď neexistují jako čisté kondenzované látky nebo neexistují jako čisté látky vůbec (např. ion
NO3– v roztoku HNO3). Aktivita je pak definována vztahem:
Xi
(3.83)
ai
i
X ist
kde Xi je koncentrace (různým způsobem vyjádřená) složky v uvažovaném stavu, Xist její koncentrace ve standardním stavu, tj. v roztoku o jednotkové koncentraci a to buď
mist = 1 mol kg–1
nebo
cist = 1 mol dm–3
(někdy se používá i standardního stavu na bázi hmotnostních procent) a předpokládáme, že aktivitní koeficient uvažované látky v tomto roztoku má limitní hodnotu, i = 1 (pro tento předpoklad
se tento standardní stav nazývá stavem nekonečného zředění, i když jde o roztok konečné koncentrace). Roztok, v němž předpokládáme jednotkové hodnoty aktivitních koeficientů je označován jako roztok ideální.
TŘETÍ VĚTA TERMODYNAMICKÁ
Na základě prvé věty termodynamické byly definovány vnitřní energie U a entalpie H, které spolu
s hodnotami tepla a práce vyměněnými při jakémkoli ději vystihují platnost principu zachování
energie. Na základě druhé věty termodynamické byly definovány entropie S , Helmholtzova energie
F a Gibbsova energie G, schopné mezi ději, jež nejsou v rozporu s prvou větou, rozlišit ještě děje,
které se uskuteční samovolně a které nikoli. Tyto funkce jsou kritériem rovnováhy a kritériem nevratnosti dějů.
Všechny tyto funkce jsou definovány až na aditivní konstantu, takže jejich absolutní hodnota
není známa. Byla proto snaha zjistit, zda u některé z nich nelze najít bod, tj. stav některého systému,
který by odpovídal její nulové hodnotě. Studium energetických změn při chemických reakcích prováděné až do velmi nízkých teplot a rozvinutí statistických představ o povaze entropie umožnilo nalézt takový bod u entropie:
Entropie každé látky v ideálním krystalickém stavu se s klesající teplotou bez omezení blíží nule:
(3.84)
lim S S0 0
T
0
Planckova formulace třetí věty termodynamické, kterou s ohledem na naše dosavadní znalosti musíme brát jako „článek víry“ (statistická termodynamika, která poskytuje exaktní důkaz nepatří do
našeho programu) umožňuje pro libovolnou látku vypočítat tzv. absolutní entropii, vztaženou ke
krystalickému stavu látky při absolutní nule. Při konstantním tlaku pro změnu entropie platí
dS = (Cp/T) dT . Podle Plancka je tedy integrační konstanta S0 v integrovaném vztahu:
T
S S0
0
Cp
T
dT
(3.85)
rovna nule. K výpočtu absolutní hodnoty entropie při teplotě T je třeba znát závislost tepelné kapacity na teplotě od teploty T do tak nízkých teplot, aby extrapolace k T = 0 byla spolehlivá. Docházíli mezi nulou a teplotou T ke změnám skupenství, je nutno ještě znát příslušné změny entalpie při
Chemická termodynamika
32
těchto fázových přeměnách. Tepelné kapacity se dnes měří běžně do nejnižší teploty 14 K. Měření
při ještě nižších teplotách je samozřejmě možné, ale je dosti nákladné; z tohoto důvodu se obvykle
závislost Cp na teplotě při nejnižších teplotách vystihuje vhodnou rovnicí, např. Debyeovým vztahem:
Cp = a T3
(3.86)
(konstanta a se vypočítá tak, že do Debyeovy rovnice dosadíme hodnotu Cp experimentálně zjištěnou při nejnižší teplotě).
Postup výpočtu absolutní entropie
Chceme např. vypočítat entropii čisté látky v plynném stavu při teplotě T a tlaku 101,325 kPa. Tato
látka se v oboru teplot 0 až Tz vyskytuje v krystalické modifikaci , při teplotě zvratu přechází na
druhou krystalickou modifikaci a při teplotě taje Tt; normální teplota varu je Tv. Kromě těchto teplotních údajů budeme k výpočtu ještě potřebovat
 teplotní závislosti molárních tepelných kapacit obou krystalických modifikací v příslušných
existenčních oborech teplot, teplotní závislost Cpm(ℓ) mezi teplotou tání a teplotou varu a teplotní
závislost Cpm(g) od teploty varu do požadované teploty T,
 změny entalpie doprovázející jednotlivé fázové přeměny, Δ zvratuHm , Δ táníHm , Δ výpHm ,
Molární entropie látky v plynném stavu při teplotě T a tlaku 101,325 kPa je pak dána vztahem
14
aT3
dT +
Sm =
T
0
Tz
C pm ( )
14
Tv
+
Ttání
T
dT +
C pm ( )
T
Obr. 3-13 Výpočet absolutní
entropie
Ttání
zvratu H m
Tz
dT +
výp H m
Tv
C pm ( )
+
T
Tz
T
+
Tv
C pm (g)
T
dT +
tání H m
Tt
+
dT
(3.87)
Cp
T
s
0 14
s
Tz

Tt
g
Tv
T
T (K)
Negativní formulace třetí věty
První i druhou větu termodynamickou je možno – mimo jiné – formulovat i „negativně“, tj. výrokem o tom, že perpetuum mobile prvního a druhého druhu není možné. I v případě třetí věty existuje určitá analogie: lze ji vyjádřit větou o nedosažitelnosti absolutní nuly:
Žádným postupem, ať jakkoli idealizovaným, nelze u žádné soustavy dosáhnout snížení její
teploty na absolutní nulu konečným počtem operací.
Stejně jako první a druhá věta, má i třetí věta v termodynamice funkci axiomu; zatímco první věta
platí absolutně, druhá věta platí pouze pro makroskopické soustavy a platnost třetí věty je omezena
pouze na „ideální krystalický stav“. Klasická termodynamika však neposkytuje vůbec žádné informace o tom, která látka je a která není v ideálním krystalickém stavu. V tom směru je třeba obrátit
se na statistickou termodynamiku.
Chemická termodynamika
33